Direkte Verfahren
Lineare Gleichungs- systeme
Zur Startseite "Einführung, Lösbarkeit, Determinanten" Gauß, LR-Zerlegung, Cholesky, Matrix-Inversion, homogene Systeme, dünn besetzte Matrix, überbestimmte Systeme, Standard-Software, Kondition, Singularität Zur Startseite "Iterationsverfahren für lineare Gleichungssysteme" Symbolische Rechnung, numerische Berechnung, Beispiele mit verschiedenen Softwareprodukten, der Backslash-Operator in Matlab Zur Startseite "Rundungsfehler, Kondition, Singularität, Skalierung" Zum Vergleich"Direkte Verfahren vs. Iterationsverfahren" Zur Startseite "Überbestimmte Gleichungssysteme"

Direkte Verfahren, iterative Verfahren

Die direkten Verfahren zur Lösung des linearen Gleichungssystems

Lineares Gleichungssystem

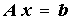
liefern nach einer endlichen Anzahl von Rechenschritten den Lösungsvektor x.

Im Gegensatz dazu suchen die iterativen Verfahren den Lösungsvektor durch sukzessive Annäherung mit einer Vektorfolge x1, x2, x3, ... , die mit einem (beliebigen) Vektor  x0 gestartet wird. Der Iterationsprozess wird abgebrochen, wenn ein iterierter Vektor xi das Gleichungssystem in einem zu definierenden Sinne ausreichend gut erfüllt.

Die wichtigsten Spezialfälle

  • Der wichtigste Fall ist das Gleichungssystem mit quadratischer und regulärer (nicht singulärer) Koeffizientenmatrix A (n Gleichungen mit n Unbekannten, der Wert der Determinante dieser Matrix muss ungleich Null sein). In diesem Fall existiert eine eindeutige Lösung des Gleichungssystems. Die Verfahren zur Lösung des Gleichungssystems müssen also die Regularität der Matrix A überprüfen (geschieht in der Regel parallel zum Berechnungsprozess).
     
  • Ein Gleichungssystem mit quadratischer singulärer Koeffizientenmatrix A kann Lösungen haben, wenn keine Widersprüche in den Gleichungen stecken. Diese Lösungen sind dann allerdings nicht eindeutig (siehe Lösbarkeit linearer Gleichungssysteme). Praktische Bedeutung hat jedoch nur der folgende Sonderfall.
     
  • Ein homogenes Gleichungssystem (siehe hierzu die spezielle Seite "Homogene Gleichungssysteme")

Homogenes Gleichungssystem

    (die rechte Seite ist der Nullvektor) hat immer (auch bei beliebiger rechteckiger Koeffizientenmatrix) die so genannte "tirviale Lösung"

    x1 = x2 = x3 = ... = xn = 0 .

    Diese ist aber in der Regel von untergeordneter Bedeutung. Ein homogenes Gleichungssystem mit quadratischer Koeffizientenmatrix kann darüber hinaus nichttriviale Lösungen haben, wenn die Koeffizientenmatrix singulär ist. Diese sind z. B. als Knickfiguren bei Stabilitätsproblemen oder als Schwingungsfiguren von Interesse (sind allerdings nicht eindeutig, so dass der Verlauf von Knick- oder Schwingungsfiguren nur qualitativ bestimmt werden kann, was bei den Aufgabenstellungen dieser Art völlig ausreichend ist, siehe hierzu: "Homogene Gleichungssysteme. Beispiel").

  • Ein überbestimmtes Gleichungssystem hat mehr Gleichungen als Unbekannte und enthält damit in der Regel Widersprüche. Hier kann eine Lösung in dem Sinne erzeugt werden, dass alle Gleichungen in einem bestimmten Sinne "bestmöglich" erfüllt werden. Dies ist die wichtige Fragestellung der Ausgleichsrechnung. Auf der Seite "Überbestimmte Gleichungssysteme" wird eine Einführung in diese Problematik gegeben.

Wegweiser zum Thema "Direkte Verfahren zur Lösung linearer Gleichungssysteme"
Home02

Homepage “Dankert/Dankert: Technische Mechanik”
Home02

Homepage “WWW - Ergänzung - Vertiefung - WWW”
Mail02

D
Mail202

nkert.de