LR-Zerlegung einer quadratischen Matrix

Bei der Entwicklung der Schritte des Gaußschen Algorithmus für die Lösung des linearen Gleichungssystems mit n Gleichungen und n Unbekannten

wird nicht deutlich, dass der Eliminationsprozess (mit dem Ziel der Triangularisierung der Koeffizientenmatrix) der Zerlegung der Matrix A in ein Produkt aus einer Links- und einer Rechts-Dreiecksmatrix entspricht. Eine solche Zerlegung, so dass bei der Rückmultiplikation entsprechend

wieder die Matrix A entsteht, ist für eine reguläre Matrix A möglich. Weil in L und R zusammen n²+n Nicht-Null-Elemente vorkommen (in beiden Matrizen sind die Hauptdiagonalen belegt), bei der Rückmultiplikation zur Erzeugung der n² Elemente von A aber nur n² Bedingungen erfüllt sein müssen, können in den Dreiecksmatrizen n Elemente frei gewählt werden. Es ist üblich (und sinnvoll), die Hauptdiagonale von L mit Einsen zu belegen.

Nebenstehend ist das Falksche Schema für die Rückmultiplikation zu sehen, das den erforderlichen Algorithmus für die Gewinnung von L und R verdeutlicht (zur Erinnerung: Jedes Element a_ij der Matrix A muss sich aus dem Skalarprodukt der i-ten Zeile von L mit der j-ten Spalte von R ergeben):

• Das Skalarprodukt aus der ersten Zeile von L mit einer beliebigen Spalte von R enthält jeweils nur ein (unbekanntes) Element r_1j von R, so dass die erste Zeile von R berechnet werden kann (wegen der 1 auf der Postion l₁₁ wird die erste Zeile von R mit der ersten Zeile von A identisch).
   
• Mit dem nun bekannten Element r₁₁ kommt in den Skalarprodukten einer beliebigen Zeile von L mit der ersten Spalte von R jeweils nur ein (unbekanntes) Element l_i1 vor, so dass die erste Spalte von L berechnet werden kann.
   
• Man setzt dieses Spiel nun mit den Skalarprodukten der zweiten Zeile von L und allen Spalten von R fort, und so entstehen immer abwechselnd die Elemente einer Zeile in R und einer Spalte in L. Der mit dem Falkschen Schema veranschaulichte Prozess kann auch durch Formeln ausgedrückt werden:

Lösen des linearen Gleichungssystems

Nach der LR-Zerlegung der Matrix A kann in dem linearen Gleichungssystem

für das Produkt aus Rechtsdreiecksmatrix R und dem Vektor der Unbekannten x ein (unbekannter) Vektor y angenommen werden (R x = y), der aus

durch so genanntes Vorwärtseinsetzen berechnet werden kann (weil L eine Dreiecksmatrix ist, kommt in der ersten Gleichung nur die Unbekannte y₁ vor, nach Berechnung von y₁ kommt in der zweiten Gleichung nur noch y₂ als Unbekannte vor usw.).

Wenn y bekannt ist, kann mit analoger Strategie der Vektor x aus

durch Rückwärtseinsetzen berechnet werden.

Einfaches Beispiel

Der oben beschriebene Algorithmus soll an dem einfachen Beispiel demonstriert werden, das auch mit dem klassischen Gauß-Algorithmus berechnet wurde:

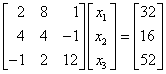
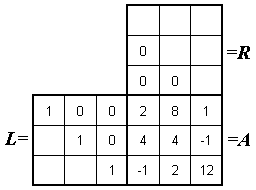
Zunächst wird die LR-Zerlegung der Matrix A durchgeführt. Das nachfolgend links zu sehende Falksche Schema ist so zu füllen, dass die Multiplikation der beiden Dreiecksmatrizen die eingetragene Matrix A ergibt:

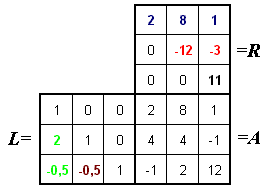
Rechts sieht man das ausgefüllte Schema. Die blauen Werte in der ersten Zeile der Rechts-Dreiecksmatrix entstehen zuerst, danach die grün eingetragenen Werte der Links-Dreiecksmatrix, dann die roten Werte usw.

Bei einem Vergleich mit dem klassischen Gauß-Algorithmus erkennt man, das die Rechts-Dreiecksmatrix exakt die dort entstandene Matrix R des "gestaffelten Systems" ist und dass die Elemente in der Links-Dreiecksmatrix exakt die Werte l_ij enthält, mit denen die einzelnen Gleichungen beim Eliminationsprozess multipliziert worden sind: Der verkettete Algorithmus ist nur eine andere Schreibweise für den klassischen Gauß-Algorithmus.

Nachfolgend ist links das Schema für das Vorwärtseinsetzen zu sehen, rechts das ausgefüllte Schema: Die Werte des Vektors y entstehen von oben nach unten ("vorwärts"), der Algorithmus entspricht exakt dem Vorgehen bei der LR-Zerlegung.

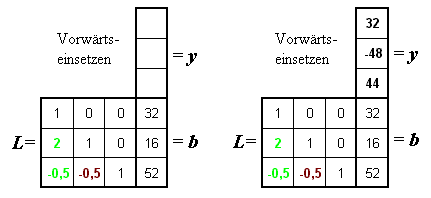
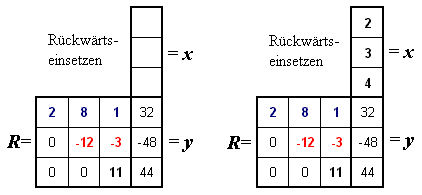
Schließlich entsteht der Lösungsvektor x durch Rückwärtseinsetzen (nachfolgend wieder links das Schema dafür, rechts das ausgefüllte Schema). Die Werte des Vektors x entstehen von unten nach oben ("rückwärts"), der Algorithmus entspricht exakt dem Rückwärtseinsetzen des klassischen Gauß-Algorithmus.

Das Falksche Schema gestattet auch hier die kompakte Anordnung aller Matrizen und Vektoren, auch hier wieder links das Schema und rechts das ausgefüllte Schema:

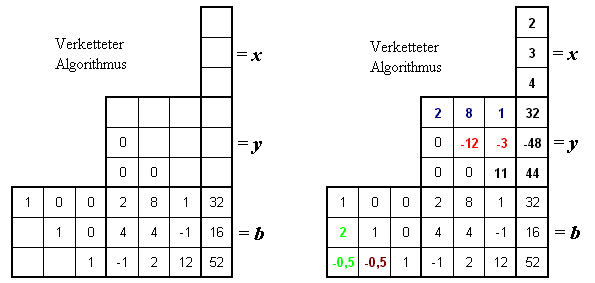
In dieser Darstellung wird besonders deutlich, dass der verkettete Algorithmus dem klassischen Gauß-Algorithmus entspricht: Das Vorwärtseinsetzen kann bei der LR-Zerlegung gleich mit erledigt werden, in dem diese auf den zusätzlichen Vektor ausgedehnt wird. Dies entspricht der Einbeziehung der rechten Seite in den Triangularisierungsprozess beim klassischen Gauß-Algorithmus. Das anschließende Rückwärtseinsetzen ist in beiden Varianten ohnehin identisch. Es ist ersichtlich, dass zusätzliche rechte Seiten einfach rechts an das Schema angefügt werden können.

Determinante, Zeilentausch, Singularität, Pivotisierung

• Der Wert der Determinante der Matrix A kann nach den Regeln für den Wert der Determinante eines Matrizenprodukts und dem Laplaceschen Entwicklungssatz entsprechend

det (A) = det (L) · det (R) = (-1)^z · r₁₁ · r₂₂ · r₃₃ · .... · r_nn

aus dem Produkt der Diagonalelemente von R berechnet werden (z ist die Anzahl der "Zeilentauschoperationen"), weil die Determinante der Links-Dreiecksmatrix L wegen der Eins-Elemente auf der Hauptdiagonalen den Wert 1 hat.

• Zeilentauschoperationen können wie beim klassischen Gauß-Algorithmus erforderlich sein, wenn ansonsten eine Division durch Null auszuführen wäre. Wenn sich keine Zeile mehr finden lässt, die diesen Mangel beheben kann, ist die Matrix A singulär, und das Gleichungssystem ist nicht eindeutig lösbar.
   
• Man sollte noch einen Schritt weiter gehen: Um den Einfluss der unvermeidlichen Rundungsfehler zu minimieren, empfiehlt sich auch für den verketteten Algorithmus die Pivotisierung in dem Sinne, dass immer mit der Zeile weitergearbeitet wird, die das betragsgrößte Hauptdiagonalelement liefert. In Rechenprogrammen brauchen dabei die Tauschoperationen nicht explizit ausgeführt zu werden, es genügt, wenn man in einem Sequenzvektor registriert, in welcher Reihenfolge die Zeilen abgearbeitet wurden (im oben demonstrierten Beispiel würde im ersten Schritt die 2. Zeile zur 1. Zeile erklärt werden (die 4 ist das betragsgrößte Element der 1. Spalte und wird so zum Hauptdiagonalelement).
   
• Die beschriebene Strategie der Pivotisierung mit fiktivem Zeilentausch kann man mit der lu-function von Matlab, die so arbeitet, sehr schön zeigen. Das folgende kleine Script zerlegt zunächst die Matrix A. Das Ergebnis im Command Window (rechts) zeigt, dass tatsächlich eine permutierte Links-Dreiecksmatrix entsteht (weil die 2. Zeile zur ersten Pivotzeile wird). Die Rückmultiplikation zur Kontrolle bestätigt, dass es eine korrekte Produktzerlegung ist.

Natrülich müsste ein anschließendes Vorwärtseinsetzen mit der 2. Zeile der Links-Dreiecksmatrix beginnen: Die Information über die Reihenfolge der Bearbeitung muss gespeichert werden. Man kann sich diese Information als zusätzlichen Ergebnisparameter der lu-function ausgeben lassen.
 

Homepage “Dankert/Dankert: Technische Mechanik”

Homepage “WWW - Ergänzung - Vertiefung - WWW”

D

nkert.de