Symbolische Rechnung, numerische Berechnung

• Programme, die symbolische Berechnungen gestatten (Mathematica, Maple, Derive, ...) können auch lineare Gleichungssysteme

lösen, wenn sich in der Koeffizientenmatrix A und/oder der rechten Seite b nichtnumerische Größen befinden. Dann finden sich diese Größen in der Regel im Ergebnisvektor x wieder, für die Unbekannten erhält man also Formeln. Dies kann sehr nützlich sein, wenn man die Einflüsse einzelner Parameter auf das Ergebnis erkennen will. Allerdings sind solche Lösungen nur bei Systemen mit einer nicht allzu großen Anzahl von Gleichungen mit erträglichem Aufwand realisierbar.

• Große Gleichungssysteme können nur numerisch gelöst werden. Es existieren zahlreiche Programme, die lineare Gleichungssysteme mit deutlich mehr als 10 000 bis weit über 1 000 000 Gleichungen lösen können. Dabei werden spezielle mathematische Eigenschaften der Koeffizientenmatrix (z. B. Symmetrie, positive Definitheit, ...) ebenso genutzt wie die Struktur der Matrix (dünne Besetzung mit von Null verschiedenen Elementen, Bandstruktur, ...). Diese Eigenschaften beeinflussen die Wahl des Lösungsverfahrens, die in der Regel der Programmbenutzer bestimmt, bei einigen Programmen aber auch der Analyse durch die Software übertragen werden kann.

Beispiele

• An einem kleinen Beispiel (drei Gleichungen mit drei Unbekannten) wird die Verwendung von mehreren Standardprogrammen demonstriert (Klicken auf das kleine Bild rechts). Dabei werden auch die Fähigkeit des jeweiligen Programms zur symbolischen Rechnung und die Reaktion auf Singularität der Koeffizientenmatrix demonstriert.
  
  
• Zwei Beispiele (Statik-Probleme, die jeweils auf 6 Gleichungen mit 6 Unbekannten führen) werden mit jeweils drei verschiedenen Programmen gelöst, wobei mindestens eine symbolische Lösung dabei ist (Klicken auf die kleinen Bilder rechts).
  
  
• An einem Statik-Problem mit 12 Gleichungen wird gezeigt, dass für ein solches Problem eine symbolische Lösung auch dann möglich ist, wenn mehrere Parameter in der Koeffizientenmatrix und der rechten Seite als Symbole verarbeitet werden müssen. Andererseits wird deutlich, dass die Anzahl der nichtnumerisch vorgegebenen Werte durchaus in Grenzen gehalten werden muss, um ein übersichtliches Ergebnis zu erhalten (Klicken auf das kleine Bild rechts).
  
  
• An einem Statik-Problem wird gezeigt, wie man die Fähigkeit der Software, auch "Überbestimmte Gleichungssysteme" lösen zu können, für die Kontrolle der Richtigkeit des aufgestellten Gleichungssystems nutzen kann (Klicken auf das kleine Bild rechts).
  
  
• An einem Finite-Elemente-Gleichungssystem mit 4482 Gleichungen werden die unterschiedlichen Speichervarianten für eine dünn mit von Null verschiedenen Elementen besetzte Koeffizientenmatrix demonstriert ("Sparse", "Band", "Skyline", Klicken auf das kleine Bild rechts).
  
  
• Ein Finite-Elemente-Gleichungssystem mit 2130 Gleichungen wird mit dem Matlab-Standard-Solver für direkte Lösungsverfahren als voll besetzte Matrix und als "Sparse matrix" gelöst (Klicken auf das kleine Bild rechts), außerdem mit dem "Präkonditionierten Konjugierte-Gradienten-Verfahren" (Iterationsverfahren).
  
  
• An mehreren Beispielen (Finite-Elemente-Gleichungssysteme) werden die 9 in Matlab angeboten iterativen Verfahren einem Vergleichstest unterzogen. Dabei werden Systeme mit 33 bis 115 921 Gleichungen gelöst (Klicken auf die kleinen Bilder rechts).

Der Backslash-Operator in Matlab, die besonders komfortable Variante

Für Matrizen ist eine Division nicht definiert. Da in Matlab alle Variablen als Matrizen betrachtet werden (skalare Größen sind 1*1-Matrizen) und für skalare Größen die Division möglich sein muss, darf das übliche Divisionssymbol (der "Slash for right division") benutzt werden. Es gibt darüber hinaus ein weiteres Divisionssymbol: Der "Backslash" führt die "inverse Division (left division)" aus, vgl. nebenstehenden Schnappschuss eines "Command Windows".

Die beiden Divisionsoperatoren / und \ sind in Matlab auch für Matrixoperationen definiert!

Sie entsprechen (wie die Operatoren für die skalaren Größen) der Umkehrung der Multiplikation, z. B. gilt:

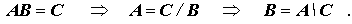
Die Backslash-Operation entspricht der Lösung eines linearen Gleichungssystems (Ax = b ⇒ x = A\b), deshalb wird diese Notation mit Abstand am häufigsten verwendet. Auch die nachfolgenden Betrachtungen beschränken sich auf die Backslash-Operation:

• Die Backslash-Operation im Sinne der "Matrix-Division" ist mit Vorsicht zu verwenden, denn für eine rechteckige (nicht quadratische) Matrix A "geht das eigentlich nicht". Dass Matlab trotzdem auch für diese Fälle (sinnvolle) Ergebnisse liefert und was dabei zu beachten ist, wird auf der Seite "Matlab: Matrix-Division, Vorsicht!" behandelt.
   
• Für die Lösung von linearen Gleichungssystemen ist der Backslash geradezu ein Zauberstab. Der Operator befreit den Anwender (scheinbar) von allen Überlegungen über den Charakter des linearen Gleichungssystems, von der Verfahrensauswahl und vielen anderen Fragen. Dass dies einerseits sehr komfortabel, andererseits aber nicht nur ein Segen ist, wird auf der Seite "Matlab: Zauberstab Backslash-Operator" besprochen.

Homepage “Dankert/Dankert: Technische Mechanik”

Homepage “WWW - Ergänzung - Vertiefung - WWW”

D

nkert.de