|
Verfahrensvergleich am einfachen praktischen Beispiel
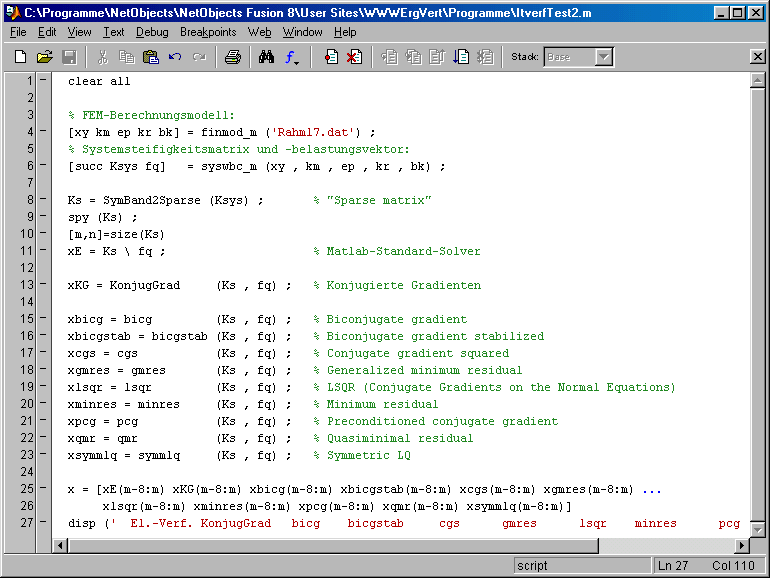
Für die Testrechnungen werden neben den 9 Matlab-Verfahren auch das weiter oben bereits verwendete Matlab-Script KonjugGrad.m verwendet. Es werden dafür FEM-Gleichungssysteme mit Matlab-Femset erzeugt (Zeilen 4 bis 6 in nachfolgendem Script ItVerfTest2.m), deren Koeffizientenmatrizen symmetrisch und positiv definit und dünn besetzt sind. Die Matrizen werden vor der Übergabe an die Lösungsalgorithmen zu "Sparse matrices" umgeformt (Zeile 8).
Die Gleichungssysteme werden zusätzlich mit dem Matlab-Standard-Solver (verwendet direkte Lösungsverfahren, Zeile 11) gelöst, um einen Vergleich mit der "exakten Lösung" zu ermöglichen.
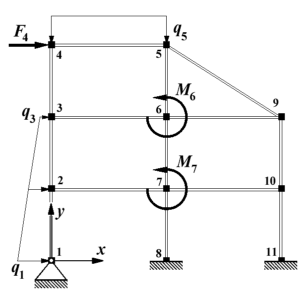
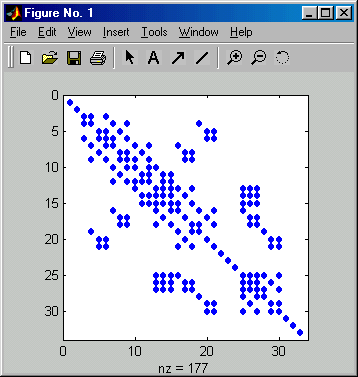
Zunächst wird ein ganz kleines Problem gelöst. Nachfolgend ist links der ebene biege- und dehnsteife Rahmen dargestellt (siehe Aufgabe B2.4 im Anhang B von "Dankert/Dankert: Technische Mechanik"), dessen FEM-Modell in der Datei Rahm17.dat gespeichert ist. Diese wird im oben zu sehenden Script in Zeile 4 geladen, das daraus erzeugte Gleichungssystem mit 33 Gleichungen hat eine Koeffizientenmatrix mit nur 177 von Null verschiedenen Elementen (siehe nachfolgend rechts zu sehendes Muster, Ausgabe der spy-Function in Zeile 9).
  Es ist ein sehr kleines System, dessen Lösung mit beliebigen Verfahren unproblematisch sein sollte. Deshalb wurden im Matlab-Script auch alle Solver mit den Default-Werten für die Parameter aufgerufen.
Das Ergebnis ist eher enttäuschend: Kein iteratives Lösungsprogramm liefert eine brauchbare Lösung für dieses Mini-System ab. Der Grund dafür ist die viel zu optimistische Voreinstellung des Parameters "Maximale Anzahl auszuführender Iterationen". In KonjugGrad.m ist dieser Wert auf 30 eingestellt, in den von Matlab angebotenen Verfahren auf 20, in einigen sogar auf 10. Die Annahme, dass damit schon eine akzeptable Näherung der Lösung zu erreichen ist, wird durch dieses kleine Beispiel widerlegt, siehe folgenden Ausschnitt des Command Windows mit der Ergebnisausgabe:
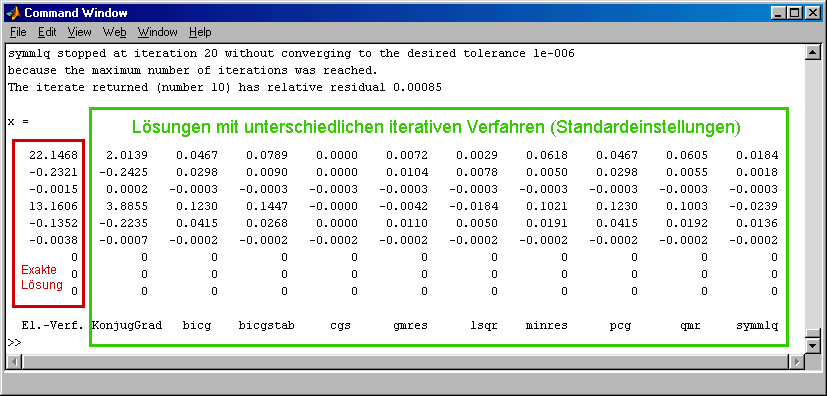
Es wurden jeweils nur die letzten 12 Werte der insgesamt 33 Elemente umfassenden Lösungsvektoren ausgegeben. Die linke Spalte ist das (korrekte) Ergebnis, das der Matlab-Standard-Solver lieferte. Keines der 10 iterativen Verfahren, deren Ergebnisse in den Spalten 2 bis 11 stehen (darunter jeweils der Name der Function) kam auch nur in die Nähe dieser Werte.
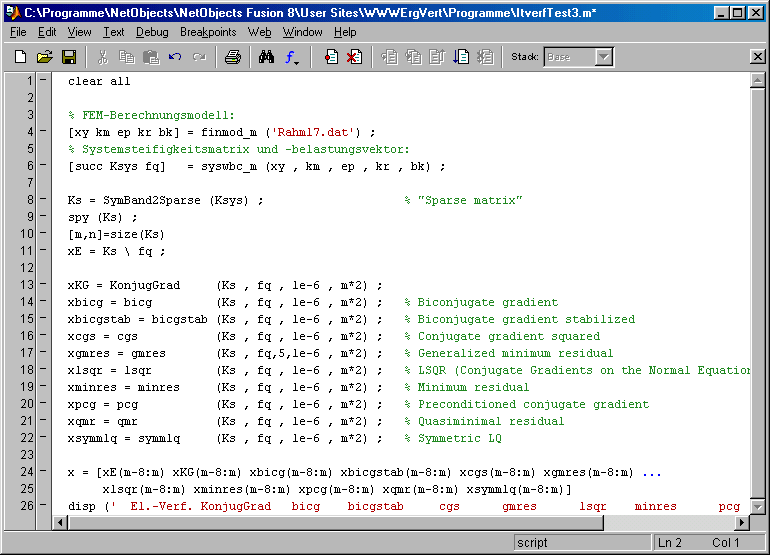
Deshalb wird die Rechnung mit einem modifizierten Matlab-Script ItverfTest3.m wiederholt, in dem den Functions für die iterativen Verfahren jeweils 2 zusätzliche Parameter übergeben werden: Auf Position 3 steht der Toleranzwert (Norm des Restvektors bezogen auf die Norm des Vektors der rechten Seite), der als Maß für die Konvergenz gilt, 10-6 ist der Standardwert, mit dem die Functions auch dann arbeiten, wenn kein Wert übergeben wird. Der 4. Parameter gibt die Anzahl der maximal auszuführenden Iterationsschritte an. Der hier gewählte Wert 2·m (m ist die Anzahl der Gleichungen) sollte eigentlich mehr als ausreichend sein, man bedenke, dass z. B. die Methode der konjugierten Gradienten theoretisch schon nach m Schritten konvergiert:
Nun sieht das Ergebnis (allerdings nur teilweise) besser aus. Deshalb wird nachfolgend die komplette Ausgabe aller Functions in das Command Window gezeigt:
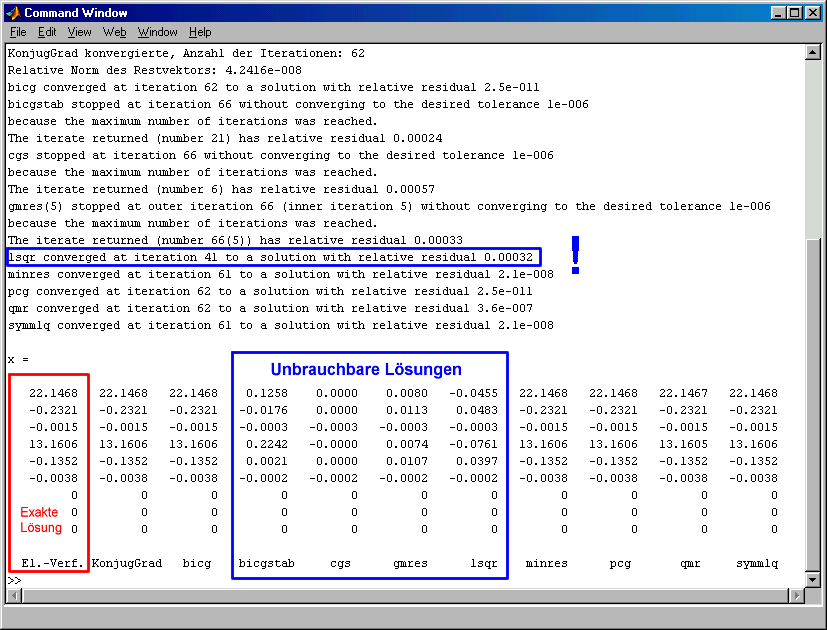
Fazit dieser Rechnungen:
- Bei dem ausgesprochen kleinen Gleichungssystem versagen alle iterativen Verfahren bei Verwendung der Standardeinstellung für die maximale Anzahl auszuführender Iterationen.
- Wenn der Wert für die maximal auszuführenden Iterationen auf den Wert 2·m gesetzt wird (m ist die Anzahl der Gleichungen, im behandelten Beispiel ist m = 33), konvergieren 6 der 10 Verfahren und liefern korrekte Ergebnisse ab, benötigen dafür aber tatsächlich fast diese Anzahl von Iterationen (im Beispiel mehr als 60).
- Drei Verfahren meldeten Misserfolg, die bis zum Abbruch erreichten Ergebnisse sind unbrauchbar.
- Katastrophal ist die Reaktion der lsqr-Function, die Konvergenz nach bereits 41 Iterationsschritten anzeigt und dann ein völlig falsches Ergebnis abliefert (siehe hierzu auch: "Matlab: Function lsqr liefert falsches Ergebnis").
- Die hier gezeigten Rechnungen wurden mit Matlab 6.5 ausgeführt. Mit Matlab 7.0 erhält man die gleichen Ergebnisse mit einer Ausnahme: gmres stürzt in Matlab 7.0 mit einer Fehlermeldung (offensichtlicher Programmierfehler) ab.
- Die Ergebnisse dieser kleinen Testrechnung könnten das Vertrauen in die iterativen Verfahren gründlich erschüttern. Deshalb werden unter "Testrechnungen für iterative Verfahren (2)" weitere Testrechnungen vorgestellt, die zum Teil deutlich günstiger ausfallen, teilweise jedoch noch schlechter. Außerdem wird auf die Verbesserung der Situation durch Präkonditionierung verwiesen.
|
Der 
