|
|
|
 |
|
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
|
|
Die Begriffe "Spezielle Matrizen" und "Dünn besetzte Matrix" (engl.: Sparse matrix) ist im Sinne von "nur auf bestimmten Positionen oder dünn mit von Null verschiedenen Elementen besetzt" zu verstehen. Solche Matrizen können platzsparend gespeichert werden, wesentlicher ist allerdings die Einsparung von Rechenzeit, die man bei Ausnutzung der dünnen Besetzung erzielen kann. Der Effekt ergibt sich naturgemäß erst beim Arbeiten mit sehr großen Matrizen, wie sie für zahlreiche Praxisprobleme (z. B. bei Finite-Elemente-Berechnungen) typisch sind.
Man unterscheidet die "regellose dünne Besetzung" und "Matrizen spezieller Formate" (dieser Begriff ist etwas irreführend, weil Matrizen natürlich immer rechteckig sind, das spezielle Format bezieht sich auf die von Null verschiedenen Elemente):
- Bei regelloser dünner Besetzung werden nur die von Null verschiedenen Elemente und zu jedem Element das Indexpaar gespeichert. Diese Variante ist z. B. in Matlab als Regelfall für "Sparse matrices" realisiert. Ein einfaches Beispiel für die Ausnutzung dieser Speichervariante findet man hier, umfangreichere Beispiele u. a. auf den Seiten "Gleichungssysteme mit dünn besetzten Matrizen" und "Große lineare Gleichunssysteme".
- Nachfolgend werden die wichtigsten speziellen Formate vorgestellt, die besonders effektiv nutzbar sind, wenn der Bereich der von Null verschiedenen Element kompakt gespeichert wird und von den Algorithmen nur dieser Bereich bearbeitet werden muss (nicht alle Operationen können spezielle Speicherformate mit Vorteil nutzen).
|
|
|
|
|
|
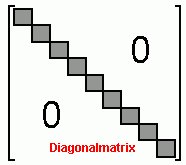 Diagonalmatrix, Einheitsmatrix Diagonalmatrix, Einheitsmatrix
Eine Diagonalmatrix hat nur auf der Hauptdiagonalen von Null verschiedene Elemente. Eine solche Matrix kann effektiv als Vektor gespeichert werden.
Ein wichtiger Spezialfall der Diagonalmatrix ist die Einheitsmatrix, deren sämtliche Diagonalelemente den Wert 1 haben. Eine Eiheitsmatrix hat bei der Matrizenmultiplikation eine ähnliche Funktion wie die skalare Eins bei der skalaren Multiplikation.
|
|
|
|
|
|
|
|
|
|
Bandmatrizen ...
... haben nur in einem relativ schmalen Band rechts und links von der Hauptdiagonalen von Null verschiedene Elemente, wobei jeweils das am weitesten von der Hauptdiagonalen entfernte Element über die rechte Bandweite IBWR bzw. linke Bandweite IBWL entscheidet. Solche Matrizen können kompakt gespeichert werden, indem man das Band "gerade rückt", wobei für die am oberen bzw. unteren Rand fehlenden Elemente Null-Elemente ergänzt werden. Die Hauptdiagonalelemente liegen bei der Kompaktspeicherung alle in einer Spalte. Weil bei den Banweiten das Hauptdiagonalelement jeweils mitgezählt wird, hat die kompakt gespeicherte Bandmatrix
N*(IBWL+IBWR-1)
Elemente. Nachfolgendes Schema zeigt dies für eine Bandmatrix mit IBWL=3 und IBWR=4:
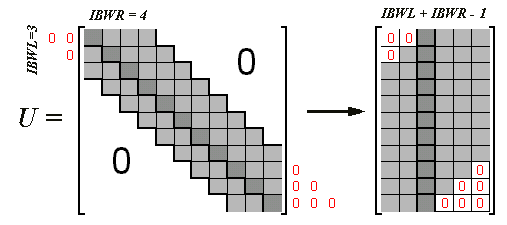
Bandmatrizen dieses Typs sind typisch für Probleme, die mit dem Differenzenverfahren gelöst werden (vgl. z. B. "Dankert/Dankert: Technische Mechank", Kapitel 18 und 19).
|
|
|
|
|
|
Symmetrische Bandmatrizen ...
... haben zusätzlich zu den oben beschriebenen Bandmatrizen die Eigenschaft, spiegelbildlich zur Hauptdiagonalen zu sein, so dass die gesamte Information durch das "halbe Band" beschrieben wird (im folgenden Schema werden dafür die Elemente auf und oberhalb der Hauptdiagonalen verwendet, so dass die Hauptdiagonale bei der Kompaktspeicherung zur 1. Spalte wird). Es gibt in diesem Fall nur eine Bandweite IBW, so dass die kompakt gespeicherte Matrix N*IBW Elemente enthält (einschließlich der ergänzenden Null-Elemente, die bei symmetrischen Bandmatrizen nur im unteren Bereich anfallen):
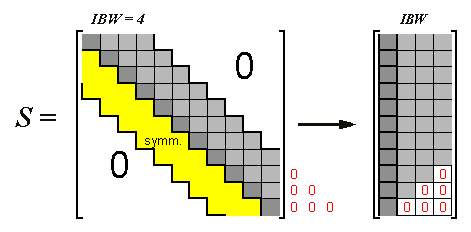
Symmetrische Bandmatrizen sind typisch für die Finite-Elemente-Methode (vgl. z. B. "Dankert/Dankert: Technische Mechank", Kapitel 16, 18, 33 und Anhang B).
|
|
|
|
|
|
Hessenberg-Form und symmetrische Tridiagonalmatrix
In der Theorie der Berechnung von Matrizeneigenwertproblemen spielen zwei besondere Matrizen eine wichtige Rolle:
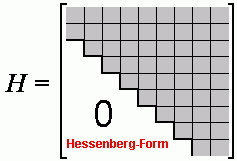 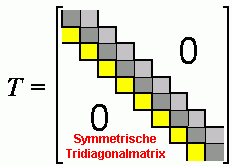
- Eine Matrix hat so genannte "Hessenberg-Form", wenn zusätzlich zur Rechtsdreiecksmatrix die Nebendiagonale unter der Hauptdiagonalen mit von Null verschiedenen Elementen besetzt ist, siehe z. B.: "Hessenberg-Form und QR-Algorithmus".
- Ein Spezialfall der Hessenberg-Form ist die symmetrische Tridiagonalmatrix, die nur auf den beiden Nebendiagonalen unmittelbar neben der Hauptdiagonalen und natürlich auf dieser von Null verschiedene Elemente hat. Wegen der Symmetrie ist die gesamte Information auf der Hauptdiagonalen und einer Nebendiagonalen enthalten.
|
|
|
 |
 |
 |
|
|
Symmetrische Skyline-Matrizen ...
... haben die von Null verschiedenen Elemente auf und über der Hauptdiagonalen, wobei für jeden "vertikalen Schornstein" eine andere Anzahl von Elementen gelten darf (Verallgemeinerung der symmetrischen Bandmatrix). Diese Matrizen werden als Satz von Vektoren (jeder Schornstein ist ein Vektor) gespeichert, deren Längen 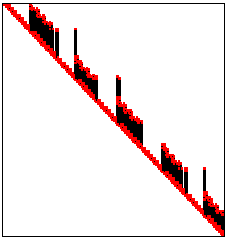 gesondert registriert werden müssen. Diese etwas aufwändig erscheinende Speicherung ist für verschiedene Berechnungsverfahren (z. B. die Cholesky-Zerlegung) sehr effektiv, wenn neue Nicht-Null-Elemente nur innerhalb der Schornsteine entstehen. gesondert registriert werden müssen. Diese etwas aufwändig erscheinende Speicherung ist für verschiedene Berechnungsverfahren (z. B. die Cholesky-Zerlegung) sehr effektiv, wenn neue Nicht-Null-Elemente nur innerhalb der Schornsteine entstehen.
Matrizen dieses Typs sind typisch für Finite-Elemente-Probleme. Im nebenstehenden Schema sind (nur für das rechte obere Dreieck der symmetrischen Matrix) die Nicht-Null-Elemente rot gezeichnet. Die schwarz gezeichneten Elemente sind in der Ausgangsmatrix Null-Elemente, werden aber im Verlauf der Berechnung (Cholesky-Zerlegung) zu Nicht-Null-Elementen (das Schema wurde vom zum freien Download verfügbaren Programm WFemset erzeugt, das auf der Basis des Finite-Elemente-Baukastens Femset geschrieben wurde).
Man vergleiche hierzu auch die Informationen auf der Seite "Band, Skyline, Sparse und Voll".
|
|
|
 |
 |
 |
|
|
Allgemeine dünn besetzte Matrizen
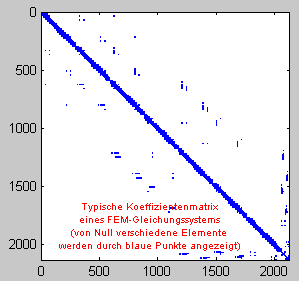 Wenn eine besondere Struktur der Nicht-Null-Elemente (wie z. B. bei Bandmatrizen) nicht vorliegt oder innerhalb einer speziellen Struktur (z. B. innerhalb des Bandes bei Bandmatrizen) auch sehr viele Null-Elemente existieren, dann können wirklich nur die Nicht-Null-Elemente und zu jedem Element das zugehörige Indexpaar (Position des Elementes in der Matrix) gespeichert werden (die Menge aller Indexpaare der Nicht-Null-Elemente wird "Besetzungsstruktur" der Matrix genannt). Es werden also z. B. drei Vektoren gleicher Länge gespeichert: Vektor a enthält kompakt alle Nicht-Null-Elemente der Matrix, Vektor i die zugehörigen Zeilennummern und Vektor j die zugehörigen Spaltennummern. Wenn eine besondere Struktur der Nicht-Null-Elemente (wie z. B. bei Bandmatrizen) nicht vorliegt oder innerhalb einer speziellen Struktur (z. B. innerhalb des Bandes bei Bandmatrizen) auch sehr viele Null-Elemente existieren, dann können wirklich nur die Nicht-Null-Elemente und zu jedem Element das zugehörige Indexpaar (Position des Elementes in der Matrix) gespeichert werden (die Menge aller Indexpaare der Nicht-Null-Elemente wird "Besetzungsstruktur" der Matrix genannt). Es werden also z. B. drei Vektoren gleicher Länge gespeichert: Vektor a enthält kompakt alle Nicht-Null-Elemente der Matrix, Vektor i die zugehörigen Zeilennummern und Vektor j die zugehörigen Spaltennummern.
Ein Beispiel für solche Speicherung einer Matrix (und die Arbeit mit dieser Matrix in Matlab nach dem Matlab-"Sparse matrix"-Konzept) findet man hier, umfangreichere Beispiele u. a. auf den Seiten "Gleichungssysteme mit dünn besetzten Matrizen" und "Große lineare Gleichunssysteme"
Eine noch etwas effektivere Speicherung folgt folgender Strategie: Die Vektoren a und i sind identisch mit der oben beschriebenen Speichervariante, der Vektor j* enthält aber nur die Positionen im Vektor i, auf der jeweils die Information für eine neue Zeile beginnt, so dass dieser Vektor in der Regel deutlich kürzer als die beiden anderen wird. Beschrieben wurde die zeilenorientierte Speicherung, analog dazu ist die spaltenorientierte Speicherung mit der Vektoren a, j und i* möglich, die die gleiche Speichermenge erfordert. In Abhängigkeit von den verwendeten Berechnungsverfahren kann eine der beiden Varianten den effektiveren Zugriff auf die Nicht-Null-Elemente ermöglichen. Es ist manchmal sogar angebracht, jeweils beide Indexvektoren zu speichern, um stets mit dem günstigeren Zugriff arbeiten zu können.
Diese Speichervarianten können trotz der zusätzlichen Index-Speicherung für sehr große sehr dünn besetzte Matrizen sehr effektiv sein, allerdings sollten dann bevorzugt Verfahren verwendet werden, bei denen die so gespeicherte Matrix möglichst nicht verändert wird (wie z. B. bei den iterativen Verfahren zur Lösung von linearen Gleichungssystemen). Matlab bietet aber auch für die so genannten direkten Verfahren zur Lösung linearer Gleichungssysteme außerordentlich effektive Algorithmen an, die mit der beschriebenen "Sparse matrix"-Speicherung arbeiten.
|
|
|
|