|
Transponierte und symmetrische Matrizen, Diagonalmatrix, Einheitsmatrix
Durch Vertauschen von Zeilen und Spalten einer Matrix A geht diese in ihre so genannte transponierte Matrix AT über:
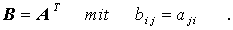
(A ist eine mn-Matrix, B dementsprechend eine nm-Matrix). Offenbar gilt:
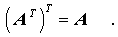
Bei quadratischen Matrizen (quadratische Matrizen haben gleiche Zeilen- und Spaltenanzahl) entspricht das Transponieren einer Spiegelung an der Hauptdiagonalen (die Hauptdiagonale einer quadratischen Matrix enthält die Elemente mit gleichen Indizes aii, sie verläuft also von links oben nach rechts unten).
Eine quadratische Matrix heißt symmetrisch, wenn sie gleich ihrer Transponierten ist. Für symmetrische Matrizen gilt also:
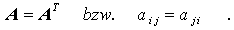
Viele Symmetrieeigenschaften physikalischer Probleme übertragen sich auf die entsprechenden Matrizen. Symmetrische Matrizen haben eine Reihe bemerkenswerter (vorteilhafter) Eigenschaften, die bei numerischen Berechnungen unbedingt genutzt werden sollten.
Eine Matrix, die nur auf der Hauptdiagonalen von Null verschiedene Elemente besitzt, heißt Diagonalmatrix D. Eine Diagonalmatrix mit durchweg gleichen Diagonalelementen dii = c heißt Skalarmatrix, weil sie sich bei der Multiplikation mit einer anderen Matrix wie ein skalarer Faktor verhält. Eine Diagonalmatrix, die ausschließlich Eins-Elemente auf der Hauptdiagonalen hat, ist eine Einheitsmatrix E, die sich bei Multiplikation mit einer anderen Matrix analog zur skalaren Eins verhält:
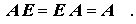
|