Überführung des Allgemeinen Matrizeneigenwertproblems in das Spezielle Matrizeneigenwertproblem

Das Allgemeine Matrizeneigenwertproblem

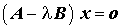
kann, wenn B regulär ist, durch Linksmultiplikation mit B^-1 auf ein Spezielles Matrizeneigenwertproblem zurückgeführt werden:

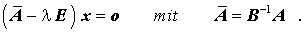
Ist B singulär, kann bei regulärer Matrix A durch Linksmultiplikation mit A^-1 auf das Spezielle Matrizeneigenwertproblem

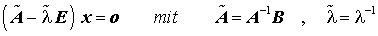
übergegangen werden, das die reziproken Eigenwerte (bei gleichen Eigenvektoren) liefert (dabei wurde die Tatsache genutzt, dass die Inverse einer Matrix die reziproken Eigenwerte der Ausgangsmatrix hat).

Wenn A und B symmetrische Matrizen sind, ist die genannte Vorgehensweise nicht empfehlenswert, da bei der Multiplikation (nicht bei der Inversion) die Symmetrie verlorengeht. Ist die symmetrische Matrix B auch noch positiv definit, so kann sie nach Cholesky entsprechend

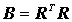
in das Produkt zweier Dreiecksmatrizen zerlegt werden. Aus

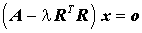
wird nach Linksmultiplikation mit der Inversen der transponierten Rechtsdreiecksmatrix und Ausklammern von R nach rechts:

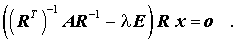
Das so entstandene Matrizeneigenwertproblem

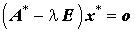
mit der Matrix

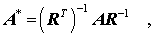
auf die sich die Symmetrieeigenschaft von A überträgt, hat die gleichen Eigenwerte wie das ursprüngliche Problem. Die Eigenvektoren x* werden gemäß

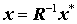
rücktransformiert. Während die Symmetrie des Matrizeneigenwertproblems in diesem Fall erhalten bleibt, geht eine eventuell vorhandene Bandstruktur der Matrix A verloren. Deshalb werden für das allgemeine Matrizeneigenwertproblem mit symmetrischen Bandmatrizen Verfahren bevorzugt, die ohne vorherige Transformation auf ein spezielles Matrizeneigenwertproblem auskommen (siehe z. B.: "Vektoriteration für das Allgemeine Eigenwertproblem").

Besonders einfach wird die Transformation, wenn B eine Diagonalmatrix ist (typischer Fall für Eigenschwingungsprobleme mit diskreten Massen). Dann wird auch R^-1 eine Diagonalmatrix D mit den Elementen

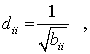
und die Transformation würde in diesem Fall auch eine Bandstruktur der Matrix A nicht zerstören.

Demonstration der Aussagen an einem Beispiel

Das auch für verschiedene andere Aussagen verwendete kleine Beispiel, dessen Hintergrund hier beschrieben wird, soll genutzt werden, um die oben gemachten Aussagen mit Matlab zu demonstrieren.

Im nebenstehend zu sehenden Script werden die beiden Matrizen in den Zeilen 3 bis 17 aufgebaut. Sie sind entsprechend der Herkunft des Problems (Finite-Elemente-Methode) symmetrisch und positiv definit und zeigen schon bei diesem kleinen Problem eine deutliche Bandstruktur.

In Zeile 22 wird entsprechend der oben beschriebenen Vorgehensweise die Inverse von B berechnet und mit A multipliziert, so dass die hier mit Aq (A-quer) bezeichnete (unsymmetrische) Matrix des äquivalenten Speziellen Matrizeneigenwertproblems entsteht:

In Zeile 27 wird B nach Cholesky zerlegt, die entstehende Rechtsdreiecksmatrix wird invertiert. Mit dem Ergebnis wird in Zeile 28 die mit As (A-Stern) bezeichnete Matrix

auf die sich die Symmetrieeigenschaft von A überträgt, erzeugt (Invertieren und Transponieren sind vertauschbar).

In den Zeilen 30 bis 32 wird die Matlab-Function eig genutzt, um zu zeigen, dass die beiden entstandenen Speziellen Matrizeneigenwertprobleme die gleichen Eigenwerte liefern wie das Allgemeine Matrizeneigenwertproblem, aus dem sie entstanden sind (der Function eig können sowohl Spezielle als auch Allgemeine Matrizeneigenwertprobleme angeboten werden). In Zeile 33 werden die berechneten Eigenwerte ausgegeben.

Der folgende Schnappschuss des Command Windows zeigt die Ergebnisse:

Man erkennt, dass die oben getroffenen Aussagen bestätigt werden:

• Die einfache Variante der Überführung des Allgemeinen Matrizeneigenwertproblems in ein Spezielles Matrizeneigenwertproblem führt auf eine unsymmetrische (hier mit Aq bezeichnete) Matrix.
   
• Die unter der Voraussetzung positiv definiter Matrix B mögliche (nur geringfügig aufwändigere) Strategie erhält die Symmetrie.
   
• In beiden Fällen aber geht die Bandstruktur des Ausgangsproblems verloren (diese Aussage gilt auch für die allgemeine Speicherung als "Sparse Matrix"). Dies kann für sehr große Matrizen ein entscheidender Nachteil sein, der nur vermieden werden kann, wenn man auf die Überführung des Allgemeinen Matrizeneigenwertproblems in ein Spezielles Matrizeneigenwertproblem verzichtet und eine Lösungsstrategie verwendet, die direkt mit dem Allgemeinen Matrizeneigenwertproblem arbeitet, zum Beispiel beschrieben auf der Seite "Inverse simultane Vektoriteration (symm. AEWP").
   
• Die abschließende Lösung der drei Matrizeneigenwertprobleme bestätigt, dass die ausgeführten Operationen auf die Eigenwerte keinen Einfluss haben. Man sollte registrieren, dass die recht komfortable Matlab-Function eig die Eigenwerte nicht in geordneter Form abliefert, was für deren weitere Verarbeitung beachtet werden muss.

Homepage “Dankert/Dankert: Technische Mechanik”

Homepage “WWW - Ergänzung - Vertiefung - WWW”

D

nkert.de