Berechnung aller Eigenwerte und Eigenvektoren
Zur Startseite "Matrizeneigenwertprobleme"
Vollständiges und partielles Matrizeneigenwertproblem, Ähnlichkeitstransformation, Satz von Schur, Vektoriteration Überführung des Allgemeinen in das Spezielle Matrizeneigenwertproblem, Wahrung der Symmetrie, Beispiel Aussagen über das Spezielle Matrizeneigenwertproblem mit symmetrischer Matrix und das Allgemeine Matrizeneigenwertproblem mit symmetrischen Matrizen Transformation auf Schursche Form, Jacobi- und Givens-Rotationen, Hessenberg-Form und QR-Algorithmus, Verfahren von Jacobi, Lösungen mit Matlab Vektoriteration nach von Mises, Rayleigh-Quotient, inverse Iteration, Vektoriteration für das Allgemeine Matrizeneigenwertproblem, Simultaniteration, Lösungen mit Matlab Matlab-Functions eig und eigs, vollständiges und partielles Matrizeneigenwertproblem, Beispiel: Eigenschwingungen eines biegesteifen Rahmens

Lösungsstrategie, Lösungsverfahren

Von den zahlreichen Lösungsverfahren, die allerdings im Wesentlichen Varianten und Modifikationen der nachfolgend genannten Verfahren sind, soll hier auf einige besonders wichtige hingewiesen werden. Weil diese sich alle auf das Spezielle Matrizeneigenwertproblem

Spezielles Matrizeneigenwertproblem mit quadratischer Matrix A und Einheitsmatrix E

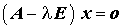
beziehen, gelten folgende Empfehlungen für Strategie und Verfahrensauswahl:

  • Wenn alle Eigenwerte (und Eigenvektoren) für das Allgemeine Matrizeneigenwertproblem

Allgemeines Matrizeneigenwertproblem mit quadratischen Matrizen A und B

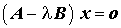
    berechnet werden sollen, ist dieses zunächst in ein Spezielles Matrizeneigenwertproblem zu überführen. Dies wird auf der Seite "Allgemeines ==> Spezielles Matrizeneigenwertproblem" beschrieben.
     

  • Für das Spezielle Matrizeneigenwertproblem mit symmetrischer Matrix liefert das Verfahren von Jacobi alle Eigenwerte und Eigenvektoren. Allerdings ist auch das nachfolgend genannte Verfahren sehr effektiv, wenn es die besonderen Vorteile der symmetrischen Matrix ausnutzt.
     
  • Für beliebige (nicht symmetrische Matrix) wird empfohlen, diese zunächst in die Hessenberg-Form zu transformieren, um danach den kompletten Satz von Eigenwerten mit dem QR-Verfahren, das die Hessenberg-Matrix in die Schursche Form transformiert, zu berechnen.

Wegweiser
Home02

Homepage “Dankert/Dankert: Technische Mechanik”
Home02

Homepage “WWW - Ergänzung - Vertiefung - WWW”
Mail02

D
Mail202

nkert.de