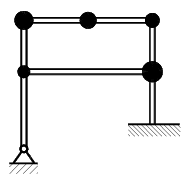In "Dankert/Dankert: Technische Mechanik" werden im Abschnitt "32.3 Eigenschwingungen linear-elastischer Systeme" zunächst Systeme betrachtet, bei denen Einzelmassen mit masselosen Federn verbunden sind (in der nebenstehenden Skizze sind dies die "Biegefedern" zwischen den Massen).

Es zeigte sich, dass ein solches System durch ein Matrizeneigenwertproblem

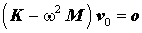
beschrieben werden kann (ω - Eigenkreisfrequenzen des Systems). M ist ein Diagonalmatrix, die die zu den Knotenverschiebungen gehörenden Einzelmassen (bzw. Massenträgheitsmomente für die Verdrehungen) enthält. K ist die Steifigkeitsmatrix des Systems, wie sie bei der Finite-Elemente-Rechnung für elastostatische Systeme entsteht. Damit bieten sich zwei Strategien für die Berechnung von Eigenschwingungen linear-elastischer Systeme an:

• Mit Hilfe des Finite-Elemente-Algorithmus wird die Systemsteifigkeitsmatrix K aufgebaut, die die Knotenverschiebungen mit den Knotenbelastungen (im Sinne der Elastostatik) verknüpft. Zu jedem Freiheitsgrad wird in einer Massenmatrix (Diagonalmatrix) eine Masse bzw. ein Massenträgheitsmoment auf der Hauptdiagonalen platziert (die Massen der Elemente können in geeigneter Form näherungsweise auf die Knotenmassen aufgeschlagen werden). Das so entstehende allgemeine Matrizeneigenwertproblem liefert Eigenkreisfrequenzen und Eigenschwingungsformen (weil M eine Diagonalmatrix ist, ist die Überführung des allgemeinen in ein spezielles Matrizeneigenwertproblem ohne nennenswerten Aufwand möglich, was die numerische Behandlung vereinfacht).
   
• Der Finite-Elemente-Algorithmus wird in dem Sinne erweitert, dass auch kontinuierlich verteilte Massen berücksichtigt werden (neben den Elementsteifigkeitsmatrizen entstehen auch Elementmassenmatrizen). Dann kann die Massenmatrix M des Systems nach dem gleichen Algorithmus wie die Steifigkeitsmatrix K aus den Elementmatrizen zusammengesetzt werden. Bei dieser (besseren) Abbildung des Schwingungssystems wird M allerdings keine Diagonalmatrix. Diese Variante wird hier behandelt.