Determinanten n-ter Ordnung
Lineare Gleichungs- systeme
Zur Startseite "Einführung, Lösbarkeit, Determinanten" Gauß, LR-Zerlegung, Cholesky, Matrix-Inversion, homogene Systeme, dünn besetzte Matrix, überbestimmte Systeme, Standard-Software, Kondition, Singularität Zur Startseite "Iterationsverfahren für lineare Gleichungssysteme" Symbolische Rechnung, numerische Berechnung, Beispiele mit verschiedenen Softwareprodukten, der Backslash-Operator in Matlab Zur Startseite "Rundungsfehler, Kondition, Singularität, Skalierung" Zum Vergleich"Direkte Verfahren vs. Iterationsverfahren" Zur Startseite "Überbestimmte Gleichungssysteme"

Definitionen

  • Einer quadratischen Matrix A (n Zeilen, n Spalten) ist eine Determinante n-ter Ordnung zuzuordnen:
     

Einer quadratischen Matrix kann immer eine Determinante zugeordnet werden

  • Streicht man in einer Determinante n-ter Ordnung die i-te Zeile und die j-te Spalte, so entsteht eine Unterdeterminante (n-1)-ter Ordnung. Multipliziert man diese mit (-1)i+j, so nennt man sie Adjunkte Aij des Elements aij.
     
  • Eine Matrix wird regulär genannt, wenn die ihr zugeordnete Determinante einen Wert ungleich Null hat, anderenfalls singulär.

Laplacescher Entwicklungssatz

Eine Determininante repräsentiert (im Gegensatz zur Matrix) einen (Zahlen-)Wert (vgl. hierzu die Betrachtungen zu Determinanten 2. Ordnung). Mit den oben gegebenen Definitionen kann dieser mit dem so genannten Laplaceschen Entwicklungssatz berechnet werden:

Berechnung des Wertes einer Determinante nach dem Laplaceschen Entwicklungssatz

  • Dies ist eine rekursive Berechnungsvorschrift: Man "entwickelt" die Determinante nach einer beliebigen Zeile oder Spalte. Dabei entstehen Unterdeterminanten, die wiederum der gleichen Vorschrift unterworfen werden.
  • Der Prozess sollte nur bis zum Entstehen von Determinanten 2. Ordnung betrieben werden, um auf diese die folgende spezielle Berechnungsvorschrift anzuwenden:

Sonderfall Determinante 2. Ordnung passt auch in die Berechnungsvorschrift des Laplaceschen Entwicklungssatzes

  • Mathematik-Programme gestatten in der Regel die Berechnung der Determinante mit einer einfachen Funktion. Nachfolgend ist die Berechnung der Determinante einer Matrix im Command Window von Matlab zu sehen:

    Beispiel: Determinantenberechnung mit Matlab
    Natürlich kann man auch Determinanten 2. Ordnung nach Laplace entwickeln. Man muss dann aber beachten, dass eine "Determinante 1. Ordnung" den Zahlenwert (einschließlich Vorzeichen) ihres einzigen Elements hat (die Symbolik der Determinante 1. Ordnung könnte leicht mit den "Absolutstrichen" verwechselt werden).

Beispiel: Die folgende Determinante 3. Ordnung wird (willkürlich) nach der 2. Zeile entwickelt, die entstehenden Unterdeterminanten 2. Ordnung werden dann nach der oben gegebenen speziellen Vorschrift berechnet:

Einfaches Beispiel: Entwicklung einer Determinate 3. Ordnung nach dem Laplaceschen Entwicklungssatz

Hinweis: Die oben mit einer Formel gegebene Festlegung für die Vorzeichen der Adjunkten entspricht einem "Schachbrettmuster" (immer links oben mit einem + beginnend), für die Determinante 3. Ordnung sieht es so aus:

Vorzeichenschema für Laplaceschen Entwicklungssatz: Schachbrettmuster

Ausnutzung spezieller Eigenschaften von Determinanten

Für die Determinanten n-ter Ordnung gelten uneingeschränkt die Eigenschaften, die für Determinanten 2. Ordnung formuliert wurden. Insbesondere die Tatsache, dass eine Determinante ihren Wert nicht ändert, wenn man das Vielfache einer Zeile (Spalte) zu einer anderen Zeile (Spalte) addiert, kann (und sollte) vor der Berechnung mit dem Laplaceschen Entwicklungssatz genutzt werden, um in der Zeile (Spalte), nach der entwickelt werden soll, möglichst viele Nullen zu erzeugen.

Bei dem oben behandelten Beispiel kann man z. B. die dritte zur ersten Zeile addieren (es entstehen zwei Nullen) und dann nach der ersten Zeile entwickeln oder das Doppelte der zweiten Spalte zur dritten Spalte addieren und dann nach der dritten Spalte entwickeln, letzteres sieht dann so aus:

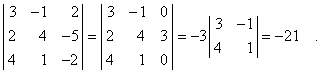
Beispiel: vereinfachung der Deteminantenberechnung durch Linearkombination von Zeilen oder Spalten

Home02

Homepage “Dankert/Dankert: Technische Mechanik”
Home02

Homepage “WWW - Ergänzung - Vertiefung - WWW”
Mail02

D
Mail202

nkert.de