Rang einer Matrix

Definition: Der Rang einer Matrix ist die maximale Anzahl ihrer linear unabhängigen Zeilen- bzw. Spaltenvektoren. Bei einer Rechteckmatrix mit m Zeilen und n Spalten kann der Rang nicht größer sein als der kleinere der beiden Werte m und n.

Durch Linearkombination von Zeilen oder Spalten einer Matrix (Multiplikation einer Zeile/Spalte mit einem Faktor und Addition oder Subtraktion zu einer anderen Zeile/Spalte) ändert sich der Rang der Matrix nicht. Der Rang einer Rechteckmatrix kann deshalb z. B. mit dem Gauß-Algorithmus ermittelt werden: Wenn die Rechnung in einer Zeile stoppt, weil in den nachfolgenden Zeilen nur noch Nullen stehen, entspricht die Nummer der "Stoppzeile" dem Rang der Matrix.

Beispiel: In einer Matrix A mit 3 Zeilen und 4 Spalten werden folgende Linearkombinationen ausgeführt:

• Von der 2. Zeile wird das 4-fache der 1. Zeile subtrahiert, von der 3. Zeile wird das 7-fache der 1. Zeile subtrahiert. Es entsteht die Matrix A₁.
• In der Matrix A₁ wird das 2-fache der 2. Zeile zur 3. Zeile addiert. Es entsteht die Matrix A₂.

Die Rechnung stoppt in der 2. Zeile, der Rang der Matrix A ist r(A) = 2.

Lösbarkeit eines linearen Gleichungssystems

Ein lineares Gleichungssystem

mit einer beliebigen rechteckigen Koeffizientenmatrix (m Gleichungen mit n Unbekannten) entsprechend

ist lösbar, wenn der Rang der Koeffizientenmatrix r(A) gleich dem Rang der um den Vektor der rechten Seite b erweiterten Matrix r(A,b) ist. Ist dieser Rang gleich der Anzahl der Unbekannten n, ist die Lösung eindeutig. Ist der Rang kleiner als die Anzahl der Unbekannten, dann können n – r(A) Unbekannte frei gewählt werden.

Für den besonders wichtigen Spezialfall der quadratischen Koeffizientenmatrix (n Gleichungen mit n Unbekannten) folgt aus dieser Aussage:

• Wenn die Koeffizientenmatrix regulär ist (nur dann ist ihr Rang gleich n, zwangsläufig auch der Rang der erweiterten Matrix), ist das Gleichungssystem in jedem Fall eindeutig lösbar.
   
• Ist die Koeffizientenmatrix singulär (ihr Rang ist kleiner als n), dann kann das Gleichungssystem Lösungen haben, diese sind dann allerdings nicht eindeutig. Wenn jedoch r(A) ≠ r(A,b) gilt, dann stecken Widersprüche in den Gleichungen, so dass das System keine Lösung hat.
   

Spezialfall "Homogenes Gleichungssystem": Ein lineares Gleichungssystem

(alle Elemente im Vektor der rechten Seite haben den Wert 0) wird homogenes Gleichungssystem genannt. Prinzipiell gelten alle oben gemachten Aussagen auch für homogene Gleichungssysteme. Weil für diesen wichtigen Sonderfall aber noch weitergehende Aussagen möglich sind, wird auf die dafür verfügbare Seite "Homogene Gleichungssysteme" verwiesen

Beispiele

Siehe auch: "Schwieriges Problem: Singularität erkennen", wo versucht wird, die hier behandelten Beispiele mit Matlab zu lösen.

Das Gleichungssystem a

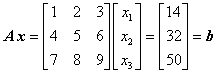
hat eine singuläre Koeffizientenmatrix (man überzeugt sich leicht, dass det(A) = 0 gilt). Für den Rang der um den Vektor b erweiterten Koeffizientenmatrix gilt:  r(A,b) = 2 (genau diese Matrix wurde oben als Beispiel für die Ermittlung des Rangs verwendet). Da aus der Beispiel-Rechnung ersichtlich ist, dass auch r(A) = 2 ist, hat dieses Gleichungssystem unendlich viele Lösungen, weil der Wert für eine Unbekannte frei gewählt werden kann. Man erhält z. B. nach einigen elementaren Umformungen (entsprechend dem oben demonstrierten Beispiel nach dem Gauß-Algorithmus):

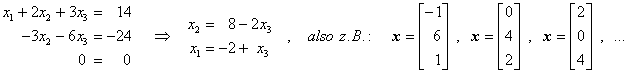
Hier wurde x₃ als die beliebig festzulegende Unbekannte gewählt, rechts sieht man eine kleine Auswahl möglicher Lösungen.

Für das nur auf der rechten Seite leicht modifizierte Gleichungssystem b

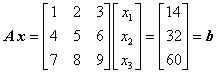
gilt dagegen: r(A) = 2 ≠ r(A,b) = 3. Deshalb hat dieses Gleichungssystem keine Lösung.

Man kann dies anschaulich so deuten:

• Gleichungssystem a enthält keinen Widerspruch, aber einen Mangel an Information, denn es sind eigentlich nur zwei Gleichungen. Man kann sofort erkennen, dass z. B. die dritte Gleichung die Differenz aus dem Doppelten der zweiten Gleichung und der ersten Gleichung ist. Damit steckt in der dritten Gleichung keine neue Information, denn Gleichungen dieser Art könnte man in beliebiger Anzahl zusätzlich aufschreiben.
   
• Gleichungssystem b dagegen enthält einen Widerspruch: Wenn man auf der linken Seite vom Doppelten der zweiten die erste Gleichung subtrahiert (dies ist die linke Seite der dritten Gleichung des Systems b), dann muss man das auf der rechten Seite auch tun, und dann erhält man 50 und nicht 60.

Rang bestimmen mit Matlab

Mit der Matlab-Function rref kann das gestaffelte System einer Matrix nach dem Verfahren von Gauß-Jordan (mit Pivotisierung) ermittelt werden. Dies ist aufwändiger und sicherer als die oben demonstrierte Handrechnung nach dem Gaußschen Algorithmus (ohne Pivotisierung). Der nebenstehend zu sehende Bildschirm-Schnappschuss zeigt das Command Window von Matlab, in dem für die oben untersuchten Matrizen (zusammengefasst zu einer Matrix mit 3 Zeilen und 5 Spalten) das gestaffelte System erzeugt wird.

Das Ergebnis bestätigt die oben durchgeführte Rechnung. Die Matrix A ist vom Rang 2, ebenso die um den Vektor b erweiterte Matrix des ersten untersuchten Gleichungssystems. Die um den Vektor b des zweiten Gleichungssystems erweiterte Matrix hat den Rang 3.

Homepage “Dankert/Dankert: Technische Mechanik”

Homepage “WWW - Ergänzung - Vertiefung - WWW”

D

nkert.de