 |
 |
 |
 |
 |
|
 |
 |
|
 |
|
 |
|
 |
|
 |
|
 |
 |
 |
 |
 |
 |
 |
|
 |
|
|
 |
|
|
|
|
|
 |
|
 |
|
 |
|
 |
|
 |
|
 |
|
 |
|
|
|
|
Basis der Strukturverbesserungen der Koeffizientenmatrix
Die Basis der Strukturverbesserungen eines Gleichungssystems mit dünn besetzter Koeffizientenmatrix sind Tauschoperationen:
- In dem linearen Gleichungssystems
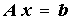
ändert sich nichts, wenn man die Zeilen in irgendeiner Weise untereinander vertauscht. Der Zeilentausch muss sich natürlich auf die Matrix A und den Vektor der rechten Seite b beziehen. Der Vektor x bleibt dabei unverändert.
- Wenn man in der Matrix A Spalten vertauscht, dann müssen auch im Vektor x die entsprechenden Positionen vertauscht werden.
Solche Zeilen- und/oder Spaltentauschoperationen werden genutzt, um die Struktur der Koeffizientenmatrix in dem Sinne zu verbessern, dass sich für die nachfolgende Lösung des Gleichungssystems mit einem direkten Verfahren die Bandweite der Matrix und/oder das Fill-in verringern. Praktisch geht man so vor:
- Zeilentausch kann beliebig vorgenommen werden, wenn sich die Operationen in gleicher Weise auf A und b beziehen.
- Spaltentausch in der Matrix A muss registriert werden, weil sich dadurch die Anordnung der Unbekannten in x ändert. Man sollte also die in A vorgenommenen Spaltentauschoperationen durch entsprechende "Rücktauschoperationen" in x nach der Lösung des Gleichungssystem wieder auf den Originalzustand des Gleichungssystems bringen (so bemerkt der Benutzer des Algorithmus nichts von diesen Operationen).
- Wenn A symmetrisch ist, sollte in jedem Fall zu jeder Zeilentauschoperation die entsprechende Spaltentauschoperation (und umgekehrt) ausgeführt werden, um die Symmetrie zu erhalten.
Beispiel: Im nachfolgend links zu sehenden Schema eines Gleichungssystems hat die (symmetrische) Matrix A die Bandweite 3 (die 6 in der 3. Spalte der 1. Zeile ist das am weitesten von der Hauptdiagonalen entfernte Nicht-Null-Element und bestimmt damit die Bandweite). Der Tausch der ersten beiden Zeilen, der auch auf der rechten Seite ausgeführt wird, verringert die rechte Bandweite, zerstört aber die Symmetrie der Matrix (mittleres Schema). Wenn nun auch die ersten beiden Spalten vertauscht werden (dabei tauschen auch die beiden Unbekannten x1 und x2 die Plätze), wird die Symmetrie der Matrix wieder hergesellt, und die Bandweite der Matrix hat sich auf den Wert 2 verringert (rechtes Schema). In diesem einfachen Beispiel ist eine Bandmatrix entstanden, die sowohl minimale Bandweite hat als auch minimales Fill-in garantiert. Nachdem das so optimierte System gelöst wurde, müssen die beiden ersten Elemente im Vektor x vertauscht werden, um den Lösungsvektor des Originalsystems zu erhalten.

|
|
|
|
|
|
Algorithmen für die Bandweiten- bzw. Fill-in-Reduktion
Das Finden geeigneter Algorithmen für die Optimierung der Bandweite ist deshalb ein besonders interessantes (und von unzähligen Autoren behandeltes) Problem,
- weil es ganz einfach zu formulieren ist (gesucht sind die Tauschoperationen, mit denen eine gegebene dünn besetzte Matrix die kleinste Bandweite bekommt) und
- weil der Algorithmus zur Lösung dieses Problems bekannt, aber nicht praktikabel ist (man braucht "nur" die n! möglichen Anordnungen der Zeilen und die n! möglichen Anordnungen der Spalten nach dem kleinsten Wert der sich ergebenden Bandweite zu durchsuchen).
Ein praktikabler Algorithmus zum Finden der optimalen Bandweite ist nicht bekannt (die Aussage bezieht sich natürlich auf große Matrizen). Sinnvoll ist ein Algorithmus zur Verringerung der Bandweite immer dann, wenn der dafür erforderliche Aufwand kleiner ist als der bei der nachfolgenden Lösung des Gleichungssystems eingesparte Aufwand.
Dies hängt auch wesentlich davon ab, ob eventuell die Bandweite des Originalsystems schon relativ gering ist. Eine solche ergibt sich bei Finite-Elemente-Berechnungen oft automatisch, wenn die Nummerierung der Knoten vom schmaleren Rand des zu untersuchenden Gebietes in "natürlicher Weise" zum gegenüberliegenden Rand verläuft. Bei mehrfach zusammenhängenden Bereichen oder örtlichen Netzverfeinerungen ist eine für die Bandweite optimale Nummerierung kaum zu erreichen, und ein geeigneter Reduktionsalgorithmus ist empfehlenswert.
Das Problem, einen geeigneten Algorithmus zu finden, um das Fill-in einer Matrix zu minimieren, die als "Sparse matrix" gespeichert ist, ist noch etwas schwieriger, aber auch auf verschiedenen Wegen in überzeugender Weise gelöst.
Für beide Probleme stehen geeignete Verfahren zur Verfügung, die einen sinnvollen Kompromiss zwischen Aufwand und Resultat erwarten lassen. Matlab bietet effektiv arbeitende Functions für alle praktisch wichtigen Fälle an. Nachfolgend werden einige Matlab-Testrechnungen für den besonders wichtigen Fall symmetrischer Koeffizientenmatrizen beschrieben.
|
|
|
|
|
|
Bandweiten- und Fill-in-Reduktion in Matlab
Hier sollen mit einem Matlab-Script die Effekte der Bandweiten- und Fill-in-Reduktion für symmetrische Matrizen gezeigt werden. Dabei wird sinnvollerweise ausschließlich mit dem Speicherformat "Sparse" gearbeitet.
Für die Bandweiten-Reduzierung einer symmetrischen Matrix A steht eine Function symrcm zur Verfügung (cm steht für Cuthill und McKee, die diesen Algorithmus bereits 1969 publizierten), der in der einfachsten Aufrufvariante die Matrix A übergeben wird, und abgeliefert wird ein Vektor r, mit dem die Umordnung in Matlab besonders einfach zu realisieren ist: Auf der i-ten Position in r steht die Zeilennummer (Spaltennummer) von A, die als i-te Zeile (Spalte) in die Matrix B, die eine reduzierte Bandweite haben wird, übernommen werden muss. Weil in Matlab die Indizes, mit den man ein Matrixelement anspricht, auch Vektoren sein dürfen, kann der gesamte Umordnungsprozess durch die Anweisungen
r = symrcm (A) ; B = A(r,r) ; c = b(r) ;
programmiert werden, und das Gleichungssystem wird dann mit der Matrix B und der rechten Seite c gelöst.
Für die Fill-in-Reduktion bietet Matlab eine nach dem gleichen Prinzip arbeitende Function symamd an.
Um die Effekte sehen zu können, muss mit der Matlab-Function chol zunächst die Cholesky-Zerlegung der Koeffizientenmatrix ausgeführt werden (bei dem Standard-Solver "Backslash" bekommt man die zerlegte Matrix nicht zu sehen). Weil chol aber nur die Zerlegung ausführt (es wird kein Gleichungssystem gelöst), wird anschließend mit zweimaligem Aufruf des "Backslash-Solvers" mit der von chol gelieferten Dreiecksmatrix das Vorwärts- und Rückwärtseinsetzen erledigt.
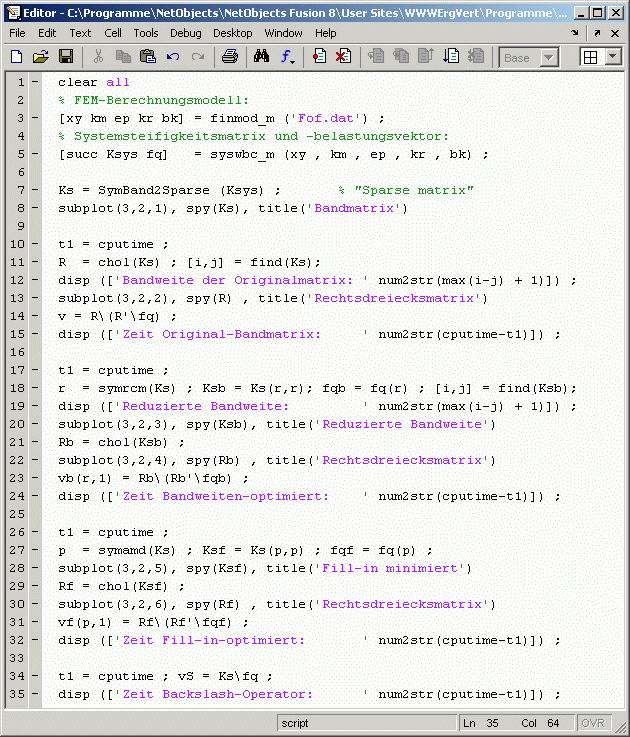 Verglichen werden die erforderlichen Rechenzeiten. In den ersten 7 Zeilen des Scripts wird das Gleichungssystem auf der Basis eines in einer Datei gespeicherten FEM-Modells erzeugt. Dies ist für die hier angestellten Betrachtungen nicht von Interesse (für Interessenten: Matlab-Femset). Die bandförmige Koeffizientenmatrix ist symmetrisch und positiv definit und wird in Zeile 7 im Speicherformat "Sparse" abgeliefert. Das Gleichungssystem wird viermal gelöst, Verglichen werden die erforderlichen Rechenzeiten. In den ersten 7 Zeilen des Scripts wird das Gleichungssystem auf der Basis eines in einer Datei gespeicherten FEM-Modells erzeugt. Dies ist für die hier angestellten Betrachtungen nicht von Interesse (für Interessenten: Matlab-Femset). Die bandförmige Koeffizientenmatrix ist symmetrisch und positiv definit und wird in Zeile 7 im Speicherformat "Sparse" abgeliefert. Das Gleichungssystem wird viermal gelöst,
- in den Zeilen 11 und 14 nach Cholesky in der vom FEM-Programm abgelieferten Form,
- in den Zeilen 21 und 23 nach Cholesky mit der Koeffizientenmatrix mit reduzierter Bandweite,
- in den Zeilen 29 und 31 nach Cholesky mit der Koeffizientenmatrix mit reduziertem Fill-in,
- in der Zeile 34 mit dem "Matlab-Standard-Solver "Backslash" in der vom FEM-Programm abgelieferten Form.
Für die 3 Lösungen nach Cholesky werden jeweils das Belegungsmuster mit Nicht-Null-Elementen für die Koeffizientenmatrix und die von der Cholesky-Zerlegung erzeugte Rechtsdreieicksmatrix graphisch dargestellt.
|
|
|
|
|
|
Testrechnung 1
 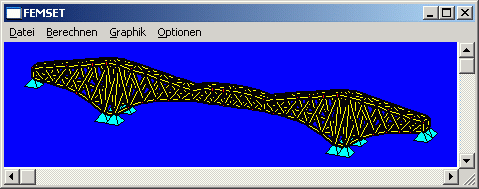
Das FEM-Modell dieser Brückenkonstruktion liefert ein Gleichungssystem mit nur 408 Gleichungen.
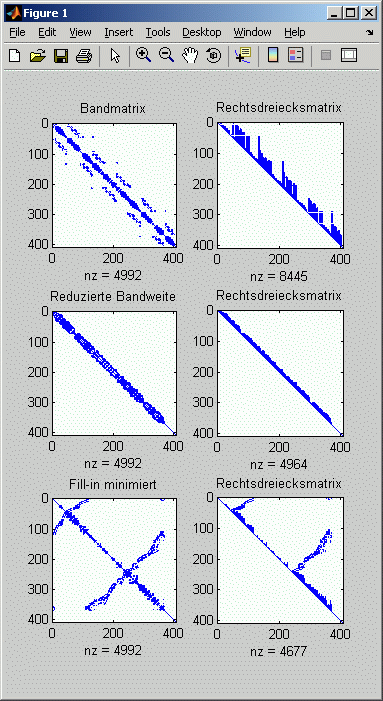
Im Bild rechts (Ausgabe der Matlab-spy-Function) sieht man links oben die Struktur der Koeffizientenmatrix, rechts daneben die Struktur der Rechtsdreiecksmatrix (Ergebnis der Cholesky-Zerlegung, schön zu sehen, dass sich die "Schornsteine" unter den Nicht-Null-Elementen füllen).
In der Mitte links ist die Matrix mit der deutlich reduzierten Bandweite zu sehen (von 93 auf 22). Dementsprechend kompakt ist das Band der Rechtsdreiecksmatrix (Mitte rechts).
Die Struktur der Fill-in-minimierten Matrix (unten links) sieht recht bizarr aus. Der jeweils als nz unter dem Bild der Rechtsdreiecksmatrix angegebene Wert für die Anzahl der Nicht-Null-Elemente zeigt aber, dass diese Rechtsdreiecksmatrix tatsächlich noch etwas dünner besetzt ist als die kompakte Bandmatrix darüber.
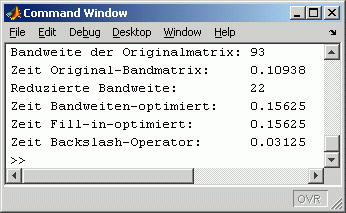
Die im Command Window abzulesenden Zeiten für die einzelnen Rechnungen zeigen: Für solch ein kleines Problem lohnt sich der Aufwand der Strukturverbesserung (trotz der deutlichen Reduzierung der Bandweite) nicht. Die Gesamtrechenzeiten für Strukturverbesserung und Lösung sind höher als die Zeit für die Berechnung mit der Originalmatrix (zum "Backslash-Operator" siehe die Bemerkung weiter unten).
|
|
|
|
|
|
Testrechnung 2
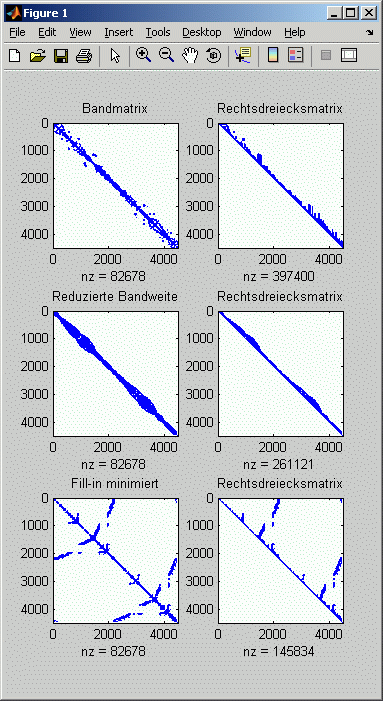 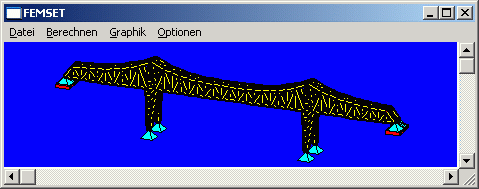
Das FEM-Modell dieser Brückenkonstruktion liefert ein Gleichungssystem mit 4482 Gleichungen.
Im Bild rechts (Ausgabe der Matlab-spy-Function) sieht man links oben die Struktur der Koeffizientenmatrix, rechts daneben die Struktur der Rechtsdreiecksmatrix (Ergebnis der Cholesky-Zerlegung).
In der Mitte links ist die Matrix mit der reduzierten Bandweite zu sehen (von 401 auf 274). Weil die Ausgangsmatrix schon eine ausgeprägte Bandstruktur hatte, ist der Gewinn nicht so groß wie beim Beispiel 1, etwas kompakter ist das Band der Rechtsdreiecksmatrix (Mitte rechts) aber doch.
Die Struktur der Fill-in-minimierten Matrix (unten links) sieht auch hier recht bizarr aus. Der jeweils als nz unter dem Bild der Rechtsdreiecksmatrix angegebene Wert für die Anzahl der Nicht-Null-Elemente zeigt aber, dass diese Rechtsdreiecksmatrix doch deutlich dünner besetzt ist als die kompakte Bandmatrix darüber.
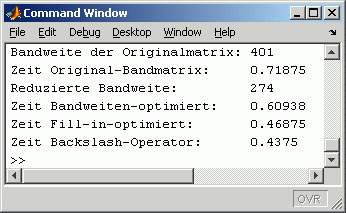
Die im Command Window abzulesenden Zeiten für die einzelnen Rechnungen zeigen: Obwohl der Gewinn nicht so groß war wie beim Beispiel 1, lohnt sich der Aufwand der Strukturverbesserung. Die Gesamtrechenzeiten für Strukturverbesserung und Lösung sind kleiner als die Zeit für die Berechnung mit der Originalmatrix (zum "Backslash-Operator" siehe die Bemerkung weiter unten).
|
|
|
|
|
|
Testrechnung 3
 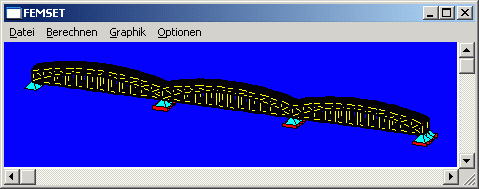
Das FEM-Modell dieser Brückenkonstruktion liefert ein Gleichungssystem mit 14652 Gleichungen.
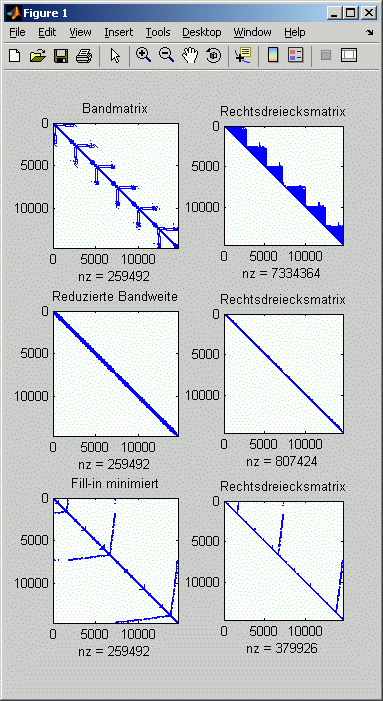
Im Bild rechts (Ausgabe der Matlab-spy-Function) sieht man links oben die Struktur der Koeffizientenmatrix, rechts daneben die Struktur der Rechtsdreiecksmatrix (Ergebnis der Cholesky-Zerlegung, schön zu sehen, dass sich die "Schornsteine" unter den Nicht-Null-Elementen füllen).
In der Mitte links ist die Matrix mit der deutlich reduzierten Bandweite zu sehen (von 2375 auf 305). Dementsprechend kompakt ist das Band der Rechtsdreiecksmatrix (Mitte rechts).
Die Struktur der Fill-in-minimierten Matrix (unten links) sieht recht bizarr aus. Der jeweils als nz unter dem Bild der Rechtsdreiecksmatrix angegebene Wert für die Anzahl der Nicht-Null-Elemente zeigt aber, dass diese Rechtsdreiecksmatrix tatsächlich noch deutlich dünner besetzt ist als die kompakte Bandmatrix darüber.
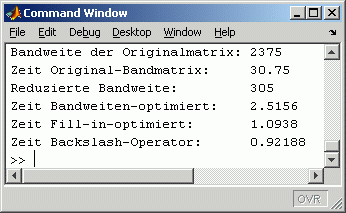
Die im Command Window abzulesenden Zeiten für die einzelnen Rechnungen zeigen: Für Problem dieser Art sollte auf die Strukturverbesserung auf keinen Fall verzichtet werden. Die Gesamtrechenzeiten für Strukturverbesserung und Lösung sind drastisch kleiner als die Zeit für die Berechnung mit der Originalmatrix (zum "Backslash-Operator" siehe die Bemerkung weiter unten).
|
|
|
|
|
|
Testsieger: Der "Backslash-Operator"
Das auffälligste Ergebnis der drei Testrechnungen mit unterschiedlichen Strukturverbesserungen der Koeffizientenmatrix ist, dass der "Matlab-Standard-Solver "Backslash" jeweils die kürzesten Rechenzeiten lieferte, obwohl ihm die Matrix mit der schlechtesten Struktur angeboten wurde. Der Grund dafür ist (siehe "Matlab: Zauberstab Backslash-Operator"):
Nach dem Aufruf des Standard-Solvers "Backslash" werden zunächst die Eigenschaften der Koeffizientenmatrix ermittelt. In diesem Fall werden Speichervariante "Sparse" und die Symmetrie festgestellt (und damit positive Definitheit vermutet, so dass das effektive Cholesky-Verfahren gewählt wird). Danach wird sicher zunächst die Fill-in-Optimierung durchgeführt, bevor der Lösungsalgorithmus gestartet wird. Der Overhead für alle diese Prüfungen ist offensichtlich geringer als der Overhead für den Aufruf mehrerer Functions.
Fazit: Mit dem Backslash-Operator steht dem Matlab-Benutzer das effektivste Werkzeug für die Lösung großer linearer Gleichungssysteme zur Verfügung. Er könnte uneingeschränkt empfohlen werden, wenn der Benutzer an die Ergebnisse des Tests der Eigenschaften der Koeffizientenmatrix herankäme. Leider aber weiß er nicht, ob der Test auf positive Definitheit positiv ausgegangen ist, weil bei negativem Ausgang sofort auf ein Verfahren umgeschaltet wird, das diese Eigenschaft nicht voraussetzt. Das ist zwar scheinbar besonders benutzerfreundlich, aber gerade der Definitheitstest ist ein besonders effektiver (und häufig einziger) Test für die Richtigkeit des zu lösenden Gleichungssystems. Man vergleiche hierzu auch die Ausführungen auf den Seiten "Matlab: Backslash, chol und linsolve" und "Matlab: Vergleich Backslash-Operator und Function chol".
|
|
|

















