|
 Hier soll exemplarisch gezeigt werden, wie die Iterationsverfahren zur Lösung linearer Gleichungssysteme auf eine schlecht konditionierte Koeffizientenmatrix reagieren.
Obwohl die Entstehung des im Folgenden betrachteten Gleichungssystem für die Betrachtungen hier unbedeutend sind, soll doch der Hintergrund mit einigen Bemerkungen verdeutlicht werden: Die Methode der finiten Elemente führt in der Regel auf lineare Gleichungssysteme mit symmetrischen, positiv definiten Koeffizientenmatrizen, die gut konditioniert sind. Dass auch diese Aussage ihre Grenzen hat, zeigt das folgende kleine Beispiel, für das die exakte Lösung bekannt ist, die auch von der Finite-Elemente-Methode geliefert werden muss, weil in diesem Fall die Ansatzfunktionen die exakte Lösung abbilden können. Das bedeutet, dass schon mit einem einzigen Element die exakte Lösung erzielt wird. Die üblicherweise mit der Anzahl der Elemente zunehmende Genauigkeit ist hier also nicht zu erwarten. Man müsste bei beliebiger Elementanzahl das exakte Ergebnis erzielen. Jede Abweichung davon ist also ausschließlich auf Rundungsfehler (in der Darstellung des Gleichungssystems und bei seiner Lösung) oder mangelde Konvergenz zurückzuführen.
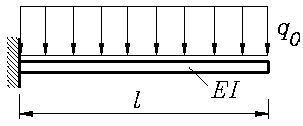 Bei einem einseitig starr eingespannten Träger der Länge l mit konstanter Biegesteifigkeit EI, der durch die konstante Linienlast q0 (z. B. sein Eigengewicht) belastet ist, senkt sich das freie Ende um
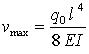
ab (vgl. z. B. "Dankert/Dankert: Technische Mechanik", Seite 245). Für die (willkürlich angenommenen) Zahlenwerte
l = 1000 mm , EI = 2 · 1010 Nmm2 , q0 = 2 N/mm
beträgt die Absenkung am freien Trägerende also
vmax = 12,5 mm .
In den Test einbezogen werden die 9 Iterationsverfahren, die in Matlab angeboten werden, und das Matlab-Script KonjugGrad.m, das im Anhang des Buchs "A. Meister: Numerik linearer Gleichungssysteme" gelistet und über den Link http://www.mathematik.uni-kassel.de/~meister/buch_online zum Download verfügbar ist.
Das nachfolgend zu sehenden Matlab-Script KondTestIter2.m baut in den Zeilen 1 bis 22 mit dem Matlab-Femset-Algorithmus das lineare Gleichungssystem mit einer symmetrischen Bandmatrix auf. Wie dies geschieht, ist für die Betrachtungen hier nicht von Belang (für Interessenten: Matlab-Femset). Von Interesse ist nur Zeile 5, in der festgelegt wird, in wieviele Elemente n der Träger eingeteilt wird und dass dabei (siehe Zeile 26) 2n+2 Gleichungen entstehen.
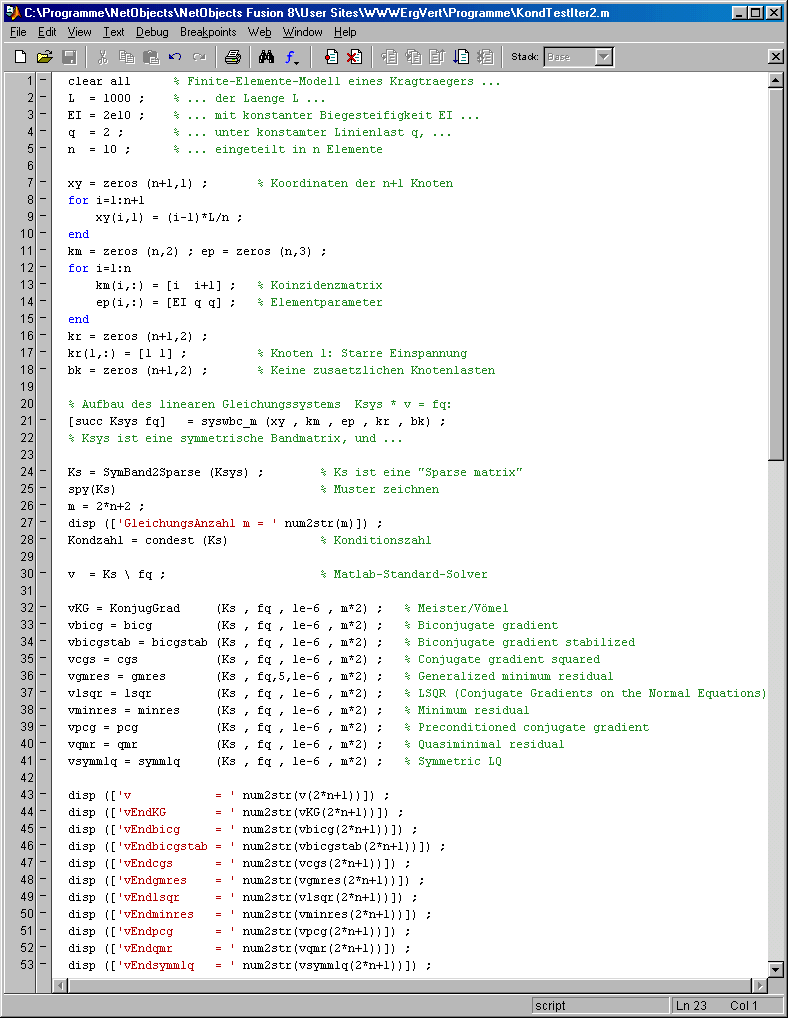
Ergebnis der Testrechnungen:
- Alle 10 Functions gestatten einen Aufruf mit nur zwei Parametern (Koeffizientenmatrix und Vektor der rechten Seite). Mit den dann verwendeten Standardwerten (je nach Verfahren maximal 20 oder 30 Iterationsschritte) wurde selbst mit dem Wert n = 10 (es wird ein Gleichungssystem mit nur 22 Gleichungen erzeugt) mit keinem der 10 Verfahren Konvergenz erzielt. Die abgelieferten Werte waren unbrauchbar, obwohl die mit condest geschätzte Konditionszahl (Zeile 28 im Script) mit einem Wert 1,7·108 in einem Bereich liegt, mit dem die direkten Verfahren noch keine Probleme haben.
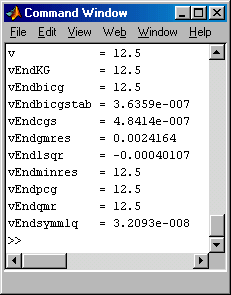 Im abgebildeten Script wurden deshalb zwei weitere Parameter an die Functions übergeben. Der Wert auf Position 3 ist der ohnehin von den Verfahren verwendete Toleranzwert für den Konvergenztest, auf Position 4 wird für die maximale Anzahl auszuführender Iterationsschritte die doppelte Anzahl der Gleichungen gestattet. Das Resultat ist enttäuschend (siehe nebenstehenden Ausschnitt aus dem Command Window): Nur 5 der getesteten 10 Verfahren melden Konvergenz, die übrigen Ergebnisse, die abgeliefert werden, sind nicht einmal in der Nähe der richtigen Lösung. Erst eine drastische Erhöhung der Anzahl der zugelassenen Iterationsschritte auf die sechsfache Anzahl der Gleichungen zeigte bei drei weiteren Verfahren Konvergenz, gmres und lsqr lieferten auch bei weiterer erheblicher Erhöhung der Anzahl der Iterationen kein brauchbares Ergebnis.
- Wenn bei einem so kleinen Gleichungssystem die Konvergenz so schlecht ist, kann man natürlich nicht erwarten, dass mit größerer Gleichungsanzahl und damit noch schlechterer Kondition der Koeffizientenmatrix vernünftige Ergebnisse erzielbar sind. Tatsächlich konvergiert bei n = 100 Elementen, die ein Gleichungssystem mit 202 Unbekannten erzeugen (Koeffizientenmatrix hat die geschätzte Konditionszahl 1,7·1010), keines der Verfahren selbst bei Zulassung von weit über 1000 Iterationsschritten. Weil sich in solchen Fällen eine Präkonditionierung geradezu aufdrängt, wird die Rechnung nachfolgend damit noch einmal ausgeführt.
|
Das Ergebnis ist erwartungsgemäß deutlich besser als bei der Rechnung ohne Präkonditionierung, allerdings auch nur bei einigen Verfahren. Diese konvergieren auch bei n = 100 Elementen (Gleichungssystem mit 202 Unbekannten), siehe nebenstehenden Ausschnitt aus dem Command Window. Der für das PKG-Verfahren ausgewiesene Wert der ausgeführten Iterationsschritte entspricht etwa der Anzahl, die auch die 5 erfolgreichen Matlab-Functions benötigten, die 4 anderen Matlab-Functions stoppten nach Erreichen der zugelassenen maximalen Anzahl von Iterationsschritten.
