
J. Dankert: Vermischte Themen zur Mathematik
Zahlen-Palindrome ("196er-Problem")
| Besuchen Sie uns bitte auf facebook |
Die Formulierung des Problems:
Eine Palindrom-Zahl kann "von rechts oder links gelesen"
werden (diese Aussage gilt natürlich auch für
"Wort-Palindrome").
Hinweis: Auf dieser Seite wird das Problem mit Dezimalzahlen
behandelt, es gibt eine ähnliche Seite für
"Binärzahlen-Palindrome".
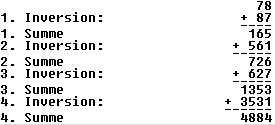
Man nehme eine beliebige positive ganze Zahl (z. B.: 83), schreibe die Ziffern in umgekehrter Reihenfolge auf (38), addiere die beiden Zahlen (83 + 38 = 121). Wenn das Ergebnis nicht gleich ein Palindrom ist, setze man das Spielchen fort (siehe nebenstehendes Beispiel für die Zahl 78), bis das Ergebnis ein Palindrom ist.
Das nachfolgende Script führt diese Rechnung aus. Man probiere es mit beliebigen Startzahlen:
Funktioniert das immer?
Wenn man mit einer beliebigen Zahl startet, stellt sich im Allgemeinen schon nach wenigen Schritten ein Palindrom ein. Mit der Startzahl 89 allerdings werden schon 24 Inversionen und Summationen benötigt, bei größeren Zahlen geht es dann wieder schneller.
Das folgende Script untersucht einen Zahlenbereich von "Anfang" bis "Ende" darauf, wie viele Inversionen benötigt werden, bis ein Palindrom entsteht. Vorsichtshalber wird wieder eine obere Grenze "Maximale Inversionen" vorgegeben, bei deren Erreichen die Rechnung abgebrochen wird (warum gerade die Voreinstellung 300 dafür vorgesehen ist, wird weiter unten deutlich). Man probiere zum Beispiel mal die Bereiche von 80 ... 110 bzw. von 180 ... 200 (wer Spaß am Scrollen hat, kann natürlich auch gleich den Bereich von 1 ... 200 oder beliebig größer untersuchen lassen):
| Anfang: | Ende: | Maximale Inversionen: | |
Bitte Werte eintragen und dann "Rechnung starten" anklicken!
Das 196er Problem
... wird so genannt, weil die 196 die kleinste Zahl ist, mit der es bisher nicht gelungen ist, ein Palindrom zu erzeugen. Es gibt aber auch keinen Beweis dafür, dass tatsächlich kein Palindrom entstehen wird. Vielleicht muss man nur hartnäckig weitersuchen.
Natürlich reizt ein solches Problem die Computer-Spezialisten. Unter http://www.p196.org wird über einige dieser hartnäckigen Sucher berichtet. Im Februar 2002 waren die Rekordhalter nach weit über 67 Millionen Inversionen bei einer Zahl mit mehr als 28 Millionen Ziffern angelangt, und die Suche ging weiter. Im Mai 2006 hat man die Zahlen mit mehr als 300 Millionen Ziffern erreicht, seitdem allerdings gibt es keine Informationen mehr von dieser Stelle.
Vieles spricht dafür, dass auch eine weitere Suche vergeblich sein wird. Schließlich wird die Wahrscheinlichkeit für das Auftreten eines Palindroms mit den länger werdenden Zahlen immer geringer. Andererseits hat man aber "unendlich viele Versuche" zur Verfügung (und der strenge mathematische Beweis dafür, dass sich die 196 tatsächlich der Regel widersetzt, existiert nicht und wird auch schwierig zu erbringen sein).
Bemerkenswert: Wenn man z. B. die Zahlen bis 10 000 untersucht, dann stellt man fest, dass es zwar 246 Zahlen gibt (das sind allerdings nicht einmal 2,5%), die sich hartnäckig widersetzen (196, 295, 394, 493, 592, 689, 691, ...), bei allen anderen Zahlen (immerhin mehr als 97,5%) stellt sich der Erfolg sehr schnell ein (die 89 ist da schon eine Ausnahme, keine der anderen "erfolgreichen" Zahlen bis 10 000 braucht mehr als 24 Schritte bis zum Erfolg).
Es drängt sich also die These auf: Entweder es funktioniert relativ schnell oder gar nicht.
Aber jenseits der 10000 gibt es schließlich doch Zahlen, die sich erst sehr hartnäckig widersetzen und dann doch ein sehr langes Palindrom liefern (z. B. wird aus 10911 erst nach 55 Inversionen: 4668731596684224866951378664). Diese Tatsache veranlasste mich einst zur
Frage im Januar 2002: Kennt jemand eine Zahl, die sich zunächst hartnäckig widersetzt und dann nach möglichst vielen Inversionen schließlich doch noch zum Palindrom wird?
Ich machte seinerzeit die Vorgabe: Die Zahl 806190001 wird nach 95 Inversionen zum 52-stelligen Palindrom 1345428953367763125675365555635765213677633598245431.
"Longest Delayed Palindrome"
Natürlich - und eigentlich hatte ich auch nichts anderes erwartet - gab es nicht nur jemand, der eine solche Zahl kennt, das Problem wurde sogar systematisch untersucht!
Am 1.3.2002 meldete sich Jason Doucette aus Kanada per E-Mail bei mir. Er behauptete (zu Recht), der "Weltrekordler" zu sein und verwies auf seine Internet-Site (sehr interessant, ein Besuch lohnt sich). Dort fand ich:
129816518702696188228910113874486338915527747725519833684478311019822881696207815618921.
Jason Doucette hatte sogar einen - wie ich finde - sehr schönen Namen für das Problem gefunden: "Longest Delayed Palindrome". In der Folgezeit meldete er mir regelmäßig neue Rekorde, den letzten am 30.11.2005:
44562665878976437622437848976653870388884783662598425855963436955852489526638748888307835667984873422673467987856626544.
Und mit dieser Zahl (nachprüfbar mit dem oben zu findenden Script) kann die Frage vom Januar 2002 wiederholt werden: Kennt jemand ein "Longer Delayed Palindrome"? Mit dem "Weltrekord" ist auch klar, warum in den Scripts jeweils 300 maximal auszuführende Inversionen als Voreinstellung gewählt wurde: Nur derjenige, der selbst auf Weltrekord-Suche gehen will, muss diesen Wert erhöhen.
