|
Ein Eigenwert λi und der zugehörige Eigenvektor xi des speziellen Matrizeneigenwertproblems
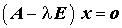
müssen offensichtlich der Beziehung
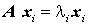
genügen. Multipliziert man diese Gleichung auf beiden Seiten von links mit dem transponierten Eigenvektor entsprechend
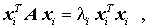
so steht auf der rechten Seite ein Skalarprodukt eines Vektors mit seinem transponierten Vektor, durch das dividiert werden kann, und man erhält:
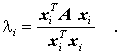
Ein Ausdruck mit einer symmetrischen Matrix A der Form
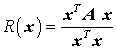
wird als Rayleighscher Quotient bezeichnet. Für einen Eigenvektor der Matrix A nimmt er den Wert des zugehörigen Eigenwertes an, und es lässt sich zeigen, dass er den Eigenwert für Vektoren x, die eine recht grobe Näherung eines Eigenvektors sind, schon sehr gut annähert (dies ist besonders für Probleme der Technischen Mechanik interessant, bei denen z. B. die Knick- bzw. Beullasten oder die Eigenfrequenzen interessieren, während die zugehörigen Knick- und Beulfiguren oder Eigenschwingungsformen von untergeordnetem Interesse sind).
Deshalb ist es empfehlenswert, die Näherungsberechnung des Eigenwertes nach der von-Mises-Iteration in jedem Iterationsschritt mit dem Rayleigh-Quotienten auszuführen, zumal der aufwändige Teil (Multiplikation Matrix · Vektor) ohnehin dem von-Mises-Iterationsschritt entspricht:
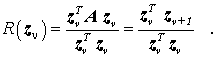
Der folgende Link zeigt ein einfaches Beispiel der Mises-Iteration für eine symmetrische Matrix unter Benutzung des Rayleigh-Quotienten.
Es lässt sich zeigen, dass
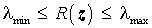
für beliebigen Vektor z gilt und dass speziell das Maximum (Minimum) des Rayleighschen Quotienten gleich dem größten (kleinsten) Eigenwert der Matrix A ist. Daraus folgt, dass der größte (kleinste) Eigenwert stets von unten (oben) genähert wird.
Für nichtsymmetrische Matrizen ist der Rayleigh-Quotient bei der von-Mises-Iteration durch
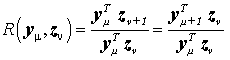
mit den so genannten "Linksiterierten" yμ ersetzen, die sich ebenfalls aus einem von-Mises-Iterationsprozess, allerdings mit der Transponierten der Matrix A entsprechend
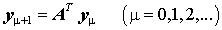
bei beliebigem Anfangsvektor y0 ergeben.
|















