|
% Energieverfahren, Aufgabe 2
clear all
% 11111111111 ANPASSEN AN DAS AKTUELLE PROBLEM VON HIER ... 111111111111111111111111111
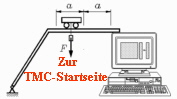
% Parameter:
a = 1000 ;
tl = 4 * a ;
E = 200000 ;
I = 40000 ;
q0 = 1 ;
F = 100 ;
M = -10000 ;
cT = 50 ;
c1 = 20 ;
c2 = 10 ;
mg = 5*9.81 ;
% Ansatzfunktionen und deren 1. und 2. Ableitungen:
m = 5 ; % Anzahl der Ansatzfuntionen (wenn m < 5 gesetzt ...
P1 = [1/tl 0] ; % ... wird, werden nur die ersten ...
P2 = [1/tl^2 0 0] ; % ... m Ansatzfunktionen verwendet)
P3 = [1/tl^3 0 0 0] ;
P4 = [1/tl^4 0 0 0 0] ;
P5 = [1/tl^5 0 0 0 0 0] ;
% 11111111111 ... BIS HIER 111111111111111111111111111111111111111111111111111111111111
P1D = polyder (P1);
P2D = polyder (P2);
P3D = polyder (P3);
P4D = polyder (P4);
P5D = polyder (P5);
P1DD = polyder (P1D) ;
P2DD = polyder (P2D) ;
P3DD = polyder (P3D) ;
P4DD = polyder (P4D) ;
P5DD = polyder (P5D) ;
% ------------------------------------------------------------------------------------
% Vorbereitung der numerischen Integration und der Ergebnisauswertung:
n = 100 ; % Anzahl der Abschnitte für numerische Integration
dz = tl / n ; % Breite eines Integrationsintervalls
nS = n + 1 ; % Anzahl der Stützstellen
zS = 0 : dz : tl ; % Koordinaten der Stützpunkte
EIS = zeros (nS , 1) ;
qS = zeros (nS , 1) ;
% 22222222222222 ANPASSEN AN DAS AKTUELLE PROBLEM VON HIER ... 222222222222222222222222
EIS(1:nS) = E * I ; % Konstante Biegesteifigkeit und ...
qS (1:nS) = mg / tl ; % ... Linienlast infolge m
ic1 = round (n/4 +1.1) ;
iF = round (n/2 +1.1) ;
iq0 = round (n*3/4+1.1) ;
for i = iF:iq0
qS(i) = qS(i) + q0 * (zS(i)-2*a)/a ;
end
for i = iq0+1:nS
qS(i) = qS(i) + q0 * (1 - (zS(i)-3*a)/a) ;
end
% 22222222222222 ... BIS HIER 222222222222222222222222222222222222222222222222222222222
% Funktionswerte und 1. und 2. Ableitung der Ansatzfunktionen an den Stützdtellen
vS (:,1) = polyval (P1 , zS)' ;
vS (:,2) = polyval (P2 , zS)' ;
vS (:,3) = polyval (P3 , zS)' ;
vS (:,4) = polyval (P4 , zS)' ;
vS (:,5) = polyval (P5 , zS)' ;
vdS (:,1) = polyval (P1D , zS)' ;
vdS (:,2) = polyval (P2D , zS)' ;
vdS (:,3) = polyval (P3D , zS)' ;
vdS (:,4) = polyval (P4D , zS)' ;
vdS (:,5) = polyval (P5D , zS)' ;
vddS(:,1) = polyval (P1DD , zS)' ;
vddS(:,2) = polyval (P2DD , zS)' ;
vddS(:,3) = polyval (P3DD , zS)' ;
vddS(:,4) = polyval (P4DD , zS)' ;
vddS(:,5) = polyval (P5DD , zS)' ;
subplot(311)
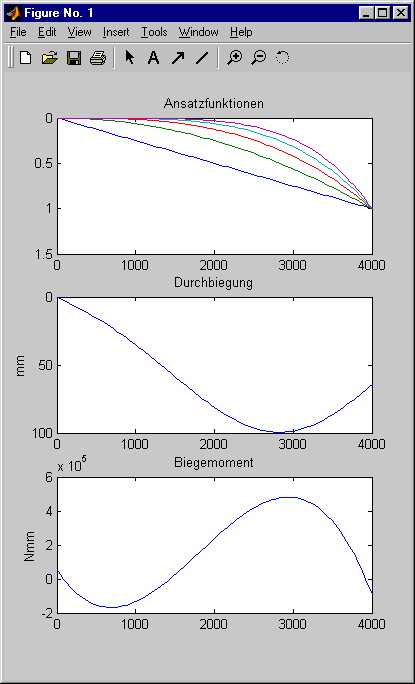
plot(zS , vS(:,1:m)) , axis ij
title('Ansatzfunktionen') ;
% ------------------------------------------------------------------------------------
% Aufbau des Gleichungssystems zur Bestimmung der Ansatzparameter:
K = zeros (m , m) ;
b = zeros (m , 1) ;
for ii = 1:m % Schleife über alle Gleichungen
Summe = (qS(1)*vS(1,ii)+qS(nS)*vS(nS,ii)) ; % Rechte Seite ...
faktor = 4 ;
for k = 2:n % Numerische Integration ...
Summe = Summe + qS(k)*vS(k,ii)*faktor ; % ... für Linienlastanteil ...
if (faktor == 4) faktor = 2 ;
else faktor = 4 ;
end ;
end
% 33333333333333 ANPASSEN AN DAS AKTUELLE PROBLEM VON HIER ... 3333333333333333333333333
b(ii) = Summe*dz/3 + F*vS(iF,ii) + M*vdS(1,ii) ; % ... + Einzelkraftanteil,
% + weitere Einzelkraftanteile + Anteile von aeusseren Momenten
% 33333333333333 ... BIS HIER ... 333333333333333333333333333333333333333333333333333333
for jj = 1:m % ii-te Zeile (Koeffizienten A)
Summe = EIS(1)*vddS(1,ii)*vddS(1,jj) + EIS(nS)*vddS(nS,ii)*vddS(nS,jj) ;
faktor = 4 ; % Numerische Integration ...
for k = 2:n % ... nach Simpsonscher Regel ...
Summe = Summe + EIS(k) * vddS(k,ii) * vddS (k,jj) * faktor ;
if (faktor == 4) faktor = 2 ; % ... für Anteil aus der ...
else faktor = 4 ; % ... Biegesteifigkeit ...
end ;
end
% 44444444444444 ANPASSEN AN DAS AKTUELLE PROBLEM VON HIER ... 4444444444444444444444444
K(ii,jj) = Summe*dz/3 + cT*vdS(1 ,ii)*vdS (1 ,jj) ... & + Drehfederanteil
+ c1*vS (ic1,ii)*vS (ic1,jj) ... % + Feder c1
+ c2*vS (nS ,ii)*vS (nS ,jj) ; % + Feder c2
% 44444444444444 ... BIS HIER ... 444444444444444444444444444444444444444444444444444444
end
end
% Lösen des Gleichungssystems
ai = zeros (5,1) ; % Maximal moegliche Zahl der Ansatzfznktionen: 5
aim = K\b ;
ai(1:m) = aim(1:m) ;
% Biegelinie graphisch darstellen:
vSchlange = vS * ai ;
subplot(312)
plot(zS , vSchlange) , axis ij
title('Durchbiegung') , ylabel('mm') ;
% Biegemoment graphisch darstellen:
v2Strich = vddS * ai ;
Mb = - EIS .* v2Strich;
subplot(313)
plot(zS , Mb) , title('Biegemoment')
ylabel('Nmm') ;
% Spezielle Werte:
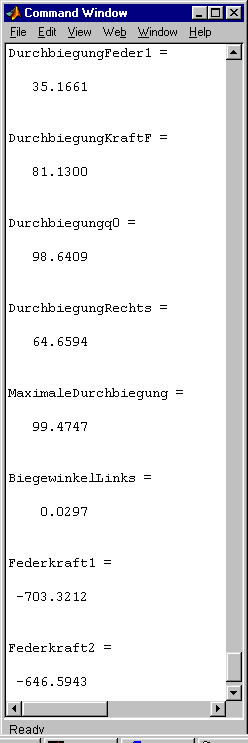
DurchbiegungFeder1 = vSchlange (ic1)
DurchbiegungKraftF = vSchlange (iF)
Durchbiegungq0 = vSchlange (iq0)
DurchbiegungRechts = vSchlange (nS)
MaximaleDurchbiegung = max(abs(vSchlange))
vStrich = vdS * ai ;
BiegewinkelLinks = vStrich (1)
Federkraft1 = -c1*vSchlange (ic1)
Federkraft2 = -c2*vSchlange (nS)
|