Die ode-Functions in Matlab

Für die numerische Integration von Anfangswertproblemen stellt Matlab insgesamt sieben Functions zur Verfügung, deren Namen mit ode beginnen (steht für "ordinary differential equations") und deren Aufruf weitgehend einheitlich ist. Die Auswahl der geeigneten Function hängt vom zu lösenden Problem und den Anforderungen an die Lösung ab. Dies stellt den Anwender meist vor kaum zu beantwortende Fragen. In der Matlab-Hilfe wird deshalb die (sehr sinnvolle) Empfehlung gegeben: "ode45 ist the best function to apply as a 'first try' for most problems". Zu ergänzen wäre vielleicht: Und wenn dieser erste Versuch fehlschlägt, dann versuche man es zunächst noch einmal (oder mehrmals) mit ode45, indem man über die "options" Einfluss auf die Berechnung nimmt.

Die folgenden Aussagen werden deshalb für die Function ode45 formuliert, gelten aber in ähnlicher und/oder sinngemäßer Art auch für die anderen Functions, zunächst aber eine an dieser Stelle besonders nachdrückliche Empfehlung:

• Die numerische Integration von Anfangswertproblemen berechnet schrittweise die Lösung für jeweils einen neuen Punkt auf der Basis von bereits ermittelten Lösungen für vorhergehende Punkte. Jedes Zwischenergebnis ist mit einem Fehler behaftet, der sich im Folgeschritt fortpflanzt. Um ein Gefühl für diesen besonders heiklen Zweig der numerischen Mathematik zu bekommen, wird dringend empfohlen, sich wenigstens grob mit den theoretischen Grundlagen vertraut zu machen, siehe z. B.: "Numerische Integration von Anfangswertproblemen".
   
• ode45 basiert auf den Formelsätzen der so genannten Runge-Kutta-Verfahren. Faktisch wird jeder Integrationsschritt doppelt gerechnet, einmal mit einer Formel 4. Ordnung, zum anderen mit einer Formel 5. Ordnung (dem so genannte Dormand-Prince-Formelpaar). Der Vergleich der beiden Ergebnisse am Ende eines Integrationsschrittes wird genutzt, um bei zu großer Differenz eine zu grobe Schrittweite zu vermuten, die dann verkleinert wird.
   
• Die durch die beschriebene Doppelrechnung ermöglichte (und in den ode-Functions realisierte) automatische Schrittweitensteuerung hat zwei wesentliche Vorteile:
• Der Anwender wird von der schwierigen Frage nach der Feinheit der Diskretisierung des Integrationsintervalls befreit.
• Eine besonders feine Schrittweite muss nur an kritischen Stellen des Integrationsintervalls realisiert werden.
   
• Trotz der komfortablen automatischen Schrittweitensteuerung wird mit der Function odeset die Möglichkeit angeboten, über Optionen das Verhalten der ode-Functions zu beeinflussen.

Automatische Schrittweitensteuerung garantiert nicht automatisch korrekte Ergebnisse

Für die Schrittweitensteuerung werden nur "lokale Informationen" (an dem Punkt, für den die Werte gerade berechnet wurden) ausgewertet. Damit kann nicht garantiert werden, dass sich über das gesamte Integrationsintervall nicht doch Fehler ergeben, die die Rechnung ungenau bis unbrauchbar machen. Und wenn erst einmal ein größerer Fehler entstanden ist, kann die weitere Rechnung nur noch unbrauchbare Ergebnisse bringen. Die dringende Empfehlung kann nur lauten:

Jede Rechnung muss auf irgendeine Weise kontrolliert werden, mindestens sollte man zwei Rechnungen mit unterschiedlichen Einstellungen für die Optionen ausführen.

Nachfolgend wird auf zwei Beispiele verwiesen, die diesen Satz bestätigen:

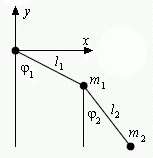• Das erste Beispiel stammt aus dem Buch von Cleve Moler: "Numerical Computing with MATLAB" (das Buch steht komplett zum Download zur Verfügung unter http://www.mathworks.com/moler/chapters.html).
  

Es ist ein einfaches Doppelpendel (zwei Punktmassen, verbunden mit masselosen starren Stangen, keine Reibung, kein Luftwiderstand). Die Differenzialgleichungen werden am Ende des Kapitels 7 hergeleitet. Die Programmierung als Matlab-Function wird ausführlich beschrieben, die Function selbst (sehr komfortabel mit Animation zeitgleich mit der Berechnung) steht unter NCM ("Numerical Computing with Matlab", http://www.mathworks.com/moler/ncmfilelist.html) als Datei swinger.m zur Verfügung.

Da ein praktisch unendliches Integrationsintervall vorgegeben ist (der Benutzer kann die Rechnung per Mausklick anhalten), wird hier die Frage untersucht: "Doppelpendel, wie lange stimmt die Rechnung?"
 

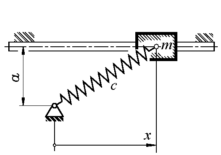• Das zweite Beispiel ist ein einfaches Feder-Masse-System mit nur einem Freiheitsgrad, das bei bestimmten Parametern in eine kritische Situation geraten können, bei der der weitere Verlauf der Bewegung von kleinen Unterschieden der berechneten Bewegungsgrößen abhängig ist. Zwei Strategien werden hier für die Kontrolle der Genauigkeit verfolgt:
  
• Man gibt die Bewegungsgrößen (Ort und Geschwindigkeit) am Ende des berechneten Intervalls aus und vergleicht so zwei Rechnungen mit unterschiedlichen Schrittweiten.
• Es wird eine zusätzliche Kontrollfunktion erzeugt (hier: Gesamtenergie im System), deren Verlauf  man als Indiz für eine "gesunde" numerische Rechnung werten kann.
   

Fazit

• Nur für sehr einfache Probleme sind die Standardeinstellungen der ode-Functions ausreichend für brauchbare Ergebnisse, ...
   
• ... aber selbst für solche Probleme hat man nach der Berechnung kaum ein Indiz für die Richtigkeit, und deshalb gilt eigentlich für alle Aufgaben die Empfehlung:
   
• Man rechne mindestens zweimal, z. B. einmal mit den Standardeinstellungen und einmal mit mit einer zwangsweise kleineren Schrittweite (gesteuert über die MaxStep-Option) und vergleiche dann die berechneten Funktionswerte am Ende des Integrationsintervalls, um gegebenenfalls (bei starken Unterschieden) eine oder mehrere weitere Berechnungen mit noch feineren Schrittweiten anzuschließen. Allgemeine Empfehlungen sind schwierig, aber mit einem MaxStep-Wert von 0,1 ist man in der Regel für den ersten Versuch gut beraten, den zweiten sollte man in Abhängigkeit von der Rechenzeit mit einem Wert zwischen 0,01 und 0,05 starten.
   
• Man starte, wenn man keine Gründe für die Verwendung eines anderen Verfahrens kennt, mit ode45. Erst dann, wenn die oben geschilderten Maßnahmen erfolglos sind, sollte man die Verwendung anderer Verfahren versuchen.

Homepage "Dankert/Dankert: Technische Mechanik"

Homepage "WWW - Ergänzung - Vertiefung - WWW"

D

nkert.de