Die nachfolgend verwendeten Differenzialgleichungen und Formeln für Biegemoment und Querkraft findet man mit Erläuterungen auf der Seite "Biegelinie für den geraden Träger, Zusammenstellung der Formeln".

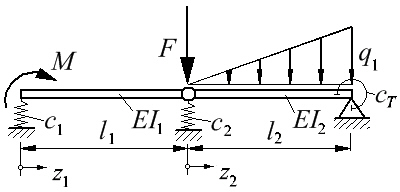Mit den in der Skizze zu sehenden Koordinaten z₁ und z₂ gelten die Differenzialgleichungen

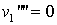
(für den linken Bereich) und

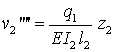
(für den rechten Bereich). Die allgemeinen Lösungen findet man jeweils durch viermaliges Integrieren:

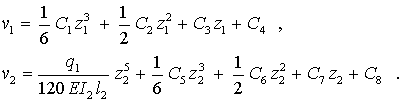
Es sind 8 Integrationskonstanten zu bestimmen. Für die Rand- und Übergangsbedingungen, in die eine Federkraft bzw. ein Federmoment eingehen, sind nachfolgende Schnittskizzen hilfreich. Für die Richtung der Federkräfte gilt: Weil positive Verschiebungen nach unten gerichtet sind (Feder wird zusammengedrückt), reagiert die Feder mit einer nach oben gerichteten Kraft. Verdrehwinkel sind bei einem solchen z-v-System im Uhrzeigersinn positiv (siehe nachfolgende Skizze rechts), so dass das von der Drehfeder auf den Träger wirkende Momente entgegen dem Uhrzeigersinn anzutragen ist:

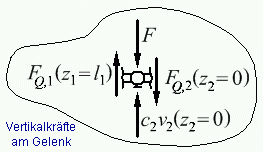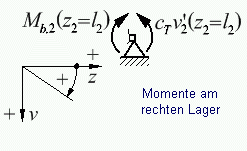
Die 8 Rand- und Übergangsbedingungen lauten:

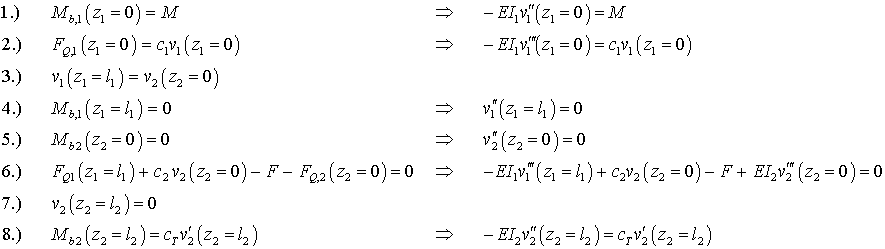
Damit kann das folgende Gleichungssystem formuliert werden:

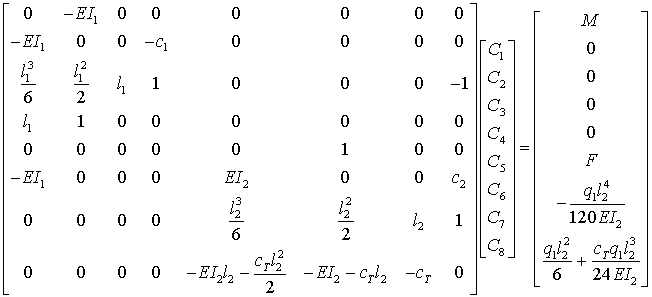
Die Lösung dieses Gleichungssystems ist (mit einiger Mühe) durchaus noch "von Hand" möglich. Weil danach die Auswertung der allgemeinen Lösung mit den dann bekannten Integrationskonstanten aber auch recht aufwändig (und alles natürlich sehr fehleranfällig) ist, kann dieser Weg kaum empfohlen werden. Das nachfolgende Matlab-Script baut das Gleichungssystem auf, löst es und wertet mit den berechneten Integrationskonstanten die Funktionen für die Durchbiegung, das Biegemoment

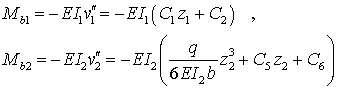
und die Querkraft

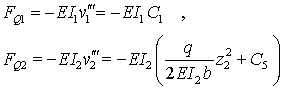
aus:

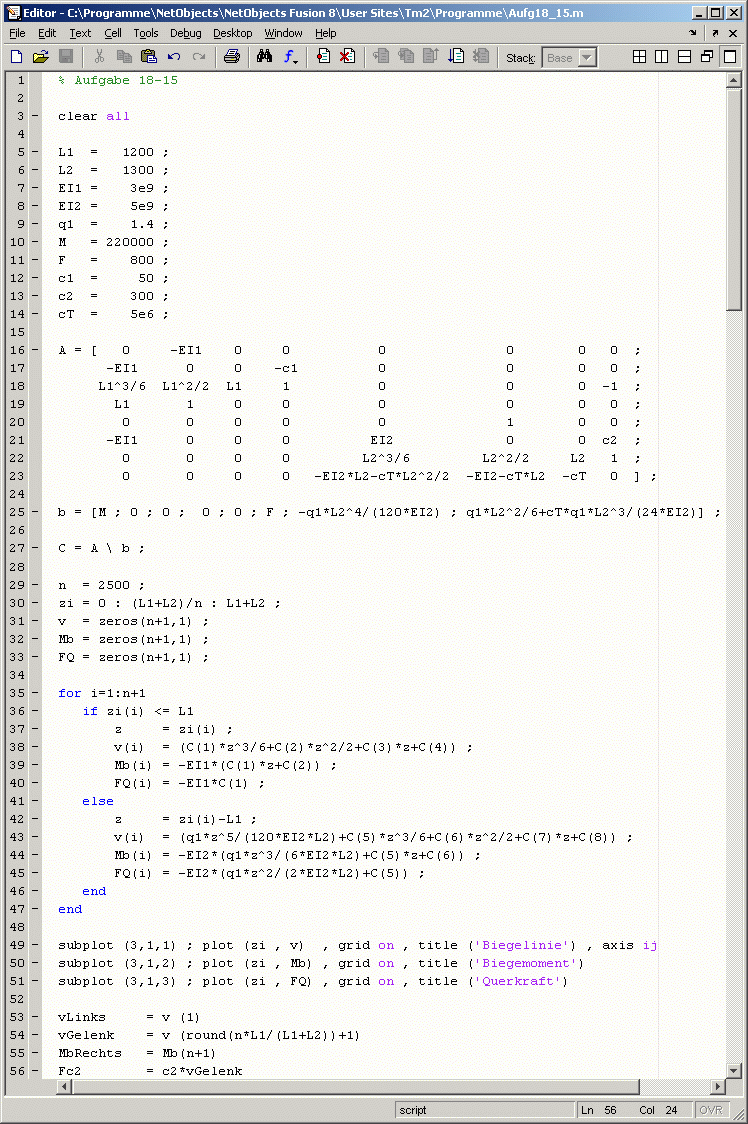
Nachfolgend sind die Ergebnisse der Rechnung zu sehen: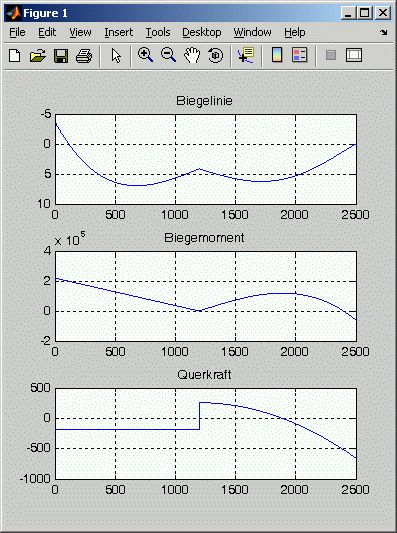

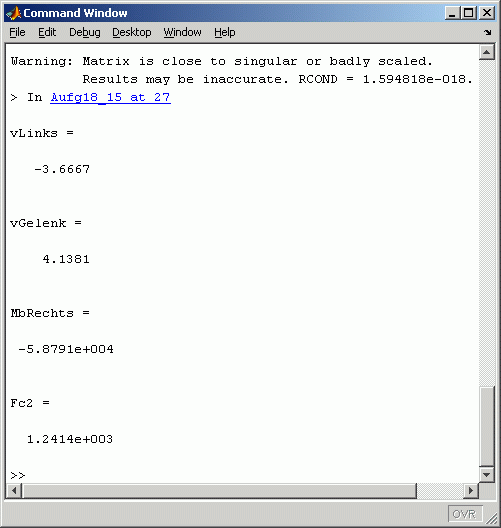
Die in das Command Window ausgegebene Warnung sollte in jedem Fall ernst genommen werden, zumal die ausgewiesene reziproke Konditionszahl die Gefahr anzeigt, dass die Ergebnisse tatsächlich unbrauchbar sein können. Außerdem ist bei einer solchen Warnung die Matrix in den meisten Fällen wirklich singulär, was bei numerischer Rechnung wegen der unvermeidbaren Rundungsfehler immer nur als "close to singular" erkannt werden kann (man vergleiche hierzu die Ausführungen auf der Seite "Rundungsfehler, Kondition, Singularität, Skalierung").

Hier liegt die Ursache bei den stark unterschiedlichen Größenordnungen der Zahlenwerte der Koeffizientenmatrix. In der dritten Zeile stehen z. B. mit dem Wert l₁³/6 auf der ersten und der 1 auf der vierten Position zwei Zahlenwerte, die sich um die Größenordnung 10⁹ unterscheiden. Man kann diesem Mangel auf mathematischem Wege z. B. über die Skalierung (siehe "Skalierung eines linearen Gleichungssystems") abhelfen, in diesem Fall aber ganz einfach durch die Rechnung mit anderen Dimensionen für die Parameter der Aufgabenstellung. Man ändert also in dem oben zu sehenden Script nur die Zeilen 5 bis 14 in dem Sinne, dass die Parameter nicht mit den Dimensionen mm und N, sondern in m und kN angegeben werden (siehe nebenstehenden Ausschnitt links).

Natürlich erhält man dann die Ergebnisse auch mit diesen Dimensionen. Der nebenstehende Ausschnitt rechts aus dem Command Window zeigt dies. Die oben zu sehende Warnung ist verschwunden, die Koeffizientenmatrix des Gleichungssystems wird nun also als ausreichend gut konditioniert angesehen. Um bei der Ausgabe von Biegeverformungen in der Dimension m überhaupt ein paar sinnvolle Stellen anzeigen zu lassen, wurde die Ausgabe auf format long umgestellt. Die Ergebnisse zeigen, dass auch mit der sehr schlecht konditionierten Matrix oben richtige Ergebnisse berechnet wurden.

Das oben zu sehende Matlab-Script ist als Aufg18_15.m bzw. in der Version mit den Dimensionen m und kN für die Parameter als Aufg18_15kNm.m zum Download verfügbar.

Zwei Warnungen

Nach den Erfahrungen, die mit dieser Aufgabe gemacht wurden, sind folgende Bemerkungen unerlässlich:

• Wenn eine Matrix als "close to singular or badly scaled" erkannt wird, sind die Ergebnisse in der Regel unbrauchbar. Dass in dem hier gezeigten Fall trotzdem richtige Ergebnisse erzielt wurden, liegt an der in dieser Hinsicht sehr ehrgeizigen Programmierung der Matlab-Functions, die andererseits allerdings sogar dazu führen kann, dass Matlab bei tatsächlich singulären Matrizen (dann natürlich unbrauchbare) Ergebnisse erzeugt, siehe dazu z. B.: "Matlab: Falsches Ergebnis für lineares Gleichungssystem".
   
• Wenn ein Fehler auftritt (und "close to singular or badly scaled" sollte immer als Fehler betrachtet werden), dann muss man nach den Ursachen suchen, und man sollte immer mit der wahrscheinlichsten Ursache beginnen. Die Ursache in dem hier behandelten Beispiel ist nicht sehr wahrscheinlich, im Gegenteil: Gerade dieser Fehler wird fast immer verursacht
   
• entweder durch einen Fehler bei der Formulierung des Gleichungssystems für ein an und für sich sinnvolles Problem oder aber
   
• bei Problemen aus der Technischen Mechanik durch den Versuch, eine Konstruktion zu berechnen (Statik-Problem oder Verformungsproblem), die aus irgendeinem Grund nicht tragfähig ist, siehe z. B.: "Singuläre Matrix, was ist die Ursache?".

www.D@nkert.de

D

nkert.de