|
 Hier soll exemplarisch gezeigt werden, wie die direkten Lösungsverfahren für lineare Gleichungssysteme auf eine schlecht konditionierte Koeffizientenmatrix reagieren.
Obwohl die Entstehung des im Folgenden betrachteten Gleichungssystem für die Betrachtungen hier unbedeutend sind, soll doch der Hintergrund mit einigen Bemerkungen verdeutlicht werden: Die Methode der finiten Elemente führt in der Regel auf lineare Gleichungssysteme mit symmetrischen, positiv definiten Koeffizientenmatrizen, die gut konditioniert sind. Dass auch diese Aussage ihre Grenzen hat, zeigt das folgende kleine Beispiel, für das die exakte Lösung bekannt ist, die auch von der Finite-Elemente-Methode geliefert werden muss, weil in diesem Fall die Ansatzfunktionen die exakte Lösung abbilden können. Das bedeutet, dass schon mit einem einzigen Element die exakte Lösung erzielt wird. Die üblicherweise mit der Anzahl der Elemente zunehmende Genauigkeit ist hier also nicht zu erwarten. Man müsste bei beliebiger Elementanzahl das exakte Ergebnis erzielen. Jede Abweichung davon ist also ausschließlich auf die Rundungsfehler (in der Darstellung des Gleichungssystems und bei seiner Lösung) zurückzuführen.
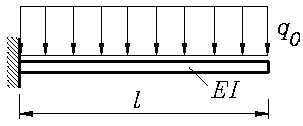 Bei einem einseitig starr eingespannten Träger der Länge l mit konstanter Biegesteifigkeit EI, der durch die konstante Linienlast q0 (z. B. sein Eigengewicht) belastet ist, senkt sich das freie Ende um
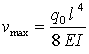
ab (vgl. z. B. "Dankert/Dankert: Technische Mechanik", Seite 245). Für die (willkürlich angenommenen) Zahlenwerte
l = 1000 mm , EI = 2 · 1010 Nmm2 , q0 = 2 N/mm
beträgt die Absenkung am freien Trägerende also
vmax = 12,5 mm .
 Das nebenstehend zu sehende Matlab-Script baut in den Zeilen 1 bis 22 mit dem Matlab-Femset-Algorithmus das lineare Gleichungssystem mit einer symmetrischen Bandmatrix auf. Wie dies geschieht, ist für die Betrachtungen hier nicht von Belang (für Interessenten: Matlab-Femset). Von Interesse ist nur Zeile 5, in der festgelegt wird, in wieviele Elemente n der Träger eingeteilt wird und dass dabei (siehe Zeile 26) 2n+2 Gleichungen entstehen.
Das Gleichungssystem wird nach zwei verschiedenen Verfahren gelöst:
- Um den Matlab-Standard-Solver verwenden zu können (Zeile 29), wird die Koeffizietenmatrix zunächst (Zeile 24) in das von Matlab unterstützte Sparse-Matrix-Format umgewandelt.
- In Zeile 33 wird der zu Matlab-Femset gehörende Solver verwendet, dem die Koeffizientenmatrix als symmetrische Bandmatrix angeboten werden muss.
In Zeile 25 wird das Muster der dünn besetzen Matrix mit der Matlab-Function spy gezeichnet. In das Command Window werden neben der Anzahl der Gleichungen (Zeile 26) und der nach beiden Verfahren berechneten maximalen Absenkungen (Zeilen 31 und 35) auch die mit der Matlab-Function condest berechnete Konditionszahl (Zeile 26) der Koeffizientenmatrix ausgegeben (Matlab kann verschiedene Konditionszahlen berechnen, für das Sparse-Matrix-Format ist allerdings nur condest verfügbar).
Nachfolgend ist die Ausgabe des Matlab-Scripts zu sehen:
 . .
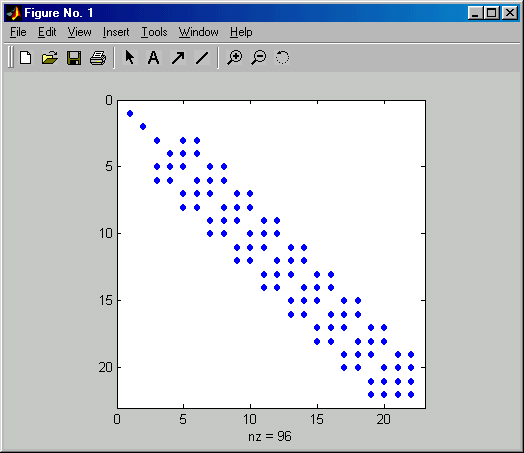Das "Belegungsmuster" der dünn besetzten Matrix zeigt, dass von den 484 Elementen der Koeffizientenmatrix mit 22 Zeilen bzw. Spalten nur 96 von Null verschieden sind. Im Command Window sieht man eine für diese relativ kleine Matrix schon recht große Konditionszahl, die auf eine schlecht konditionierte Matrix hinweist. Dies wirkt sich in diesem Fall allerdings bei beiden Gleichungssystemlösern nur in den den letzten 4 Stellen der mit 16 Dezimalstellen durchgeführten Rechnung aus.
Durch Änderung des Wertes n in der Zeile 5 des Matlab-Scripts kann die Anzahl der Gleichungen des linearen Gleichungssystems beliebig verändert werden. Die nachfolgende Tabelle zeigt eine Zusammenstellung der Ergebnisse verschiedener Rechnungen (es werden 15 wesentliche Dezimalstellen angegeben):
|
n
(Anzahl der
Elemente)
|
Anzahl der
Gleichungen des
Gleichungssystems
|
Konditionszahl
|
vend
(Lösung mit
Matlab-Solver)
|
vend
(Lösung mit
Femset-Solver)
|
|
1
|
4
|
1,3 · 106
|
12,5000000000000
|
12,5000000000000
|
|
10
|
22
|
1,7 · 108
|
12,4999999999729
|
12,5000000000092
|
|
100
|
202
|
1,7 · 1010
|
12,4999999605807
|
12,4999999605110
|
|
1000
|
2002
|
7,5 · 1012
|
12,5000828935572
|
12,5001987346142
|
|
10000
|
20002
|
1,2 · 1017
|
25,1408513728516
|
Meldung:
“Koeffizientenmatrix
ist nicht
positiv definit”
|
|
20000
|
40002
|
1,9 · 1018
|
-25,0189313590242
|
|
Die Konditionszahlen werden mit größeren Koeffizientenmatrizen zunehmend größer, die Ergebnisse dementsprechend schlechter, ab etwa 5000 Gleichungen kann man sie als unbrauchbar bezeichnen (die Größenordnungen der Konditionszahlen lassen bei Rechnung mit etwa 16 Dezimalstellen nichts anderes erwarten). Die beiden verwendeten Solver reagieren unterschiedlich:
- Der Standard-Solver von Matlab hat den Ehrgeiz, auch für sehr schlecht konditionierte Matrizen ein Ergebnis abzuliefern. Das ist für den Anwender eine sehr gefährliche Situation. Für die beiden in den letzten Tabellenzeilen verzeichneten Ergebnisse werden tatsächlich ohne Warnung unsinnige Ergebnisse abgeliefert (der negative Wert in der letzten Zeile würde bedeuten, dass sich der Träger unter der nach unten gerichteten Belastung nach oben durchbiegt).
- Die Meldung des Femset-Solvers ist natürlich auch nur in dem Sinne korrekt, dass der Test auf die positive Definitheit der Koeffizientenmatrix während der Berechnung (es dürfen nur positive Hauptdiagonalelemente bei der Cholesky-Zerlegung entstehen) infolge der Rundungsfehler schließlich negativ ausfällt (ohne Anfangsabbrechfehler ist die Matrix natürlich positiv definit). Immerhin wird kein unsinniges Ergebnis abgeliefert.
|
