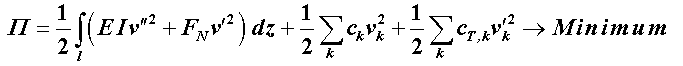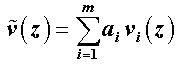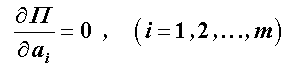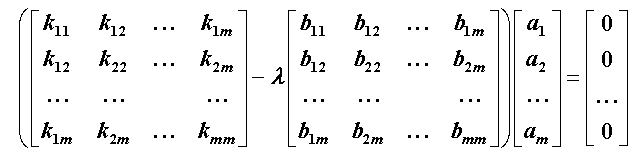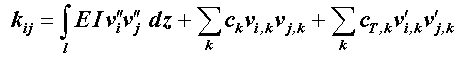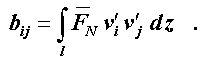|
||||||||||||||||||||||||
 |
||||||||||||||||||||||||
|
||||||||||||||||||||||||
|
Das Verhalten eines Knickstabs mit der (veränderlichen) Biegesteifigkeit EI, der durch die (veränderliche) Normalkraft FN belastet ist, wird durch die Differenzialgleichung 4. Ordnung
beschrieben (vgl. Seite 395). Sie ist ein Sonderfall der Differenzialgleichung (33.38), für die ein Randwertproblem nach der Aussage auf Seite 643 durch ein äquivalentes Variationsproblem nach (33.39) ersetzt werden kann. In diesem Fall führt dies auf
(als Energieanteile Wi*, die nicht über den Integralausdruck erfasst werden, wurden hier die Formänderungsarbeiten, die in Federn bzw. Drehfedern gespeichert werden können, berücksichtigt). Ein RITZscher Ansatz
(Ansatzfunktionen vi müssen jede für sich die geometrischen Randbedingungen erfüllen) führt über die Minimalbedingungen
auf ein ”Allgemeines symmetrisches Matrizen-Eigenwertproblem”:
mit
und
Dabei wurde aus der Funktion für die Normalkraft FN entsprechend
der Faktor -λ herausgezogen. Die Lösung des Matrizen-Eigenwertproblems liefert die λ-Werte, für die das homogene Gleichungssystem nichttriviale Lösungen hat. Der kleinste λ -Wert beschreibt dann den kritischen Zustand (Stab knickt). Für den mit Abstand häufigsten Fall einer konstanten Normalkraft infolge einer äußeren Kraft F entsprechend
vereinfacht sich damit die oben angegebene Formel für bij , weil
gesetzt werden darf, und es gilt für diesen Fall
(Eigenwert ist gleich der äußeren Kraft), dass der kleinste Eigenwert, den das Matrizen-Eigenwertproblem liefert, gleich der kritischen Last Fkr ist. Diesen Algorithmus (einschließlich Lösung des Matrizen-Eigenwertproblems) realisiert das Matlab-Script für das einfache Beispiel “Aufgabe 33-13”. Dabei werden die Integrale numerisch nach der Simpson-Regel (mit beliebig fein einstellbarer Anzahl der Integrationsabschnitte) gelöst. |
||||||||||||||||||||||||
|
|
||||||||||||||||||||||||