 |
|||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||
|
basieren auf der Idee, im Integrationsintervall Punkte auf der Kurve y(x) zu berechnen, durch diese Punkte ein oder mehrere einfache Funktionen zu legen (in der Regel Polynomfunktionen) und dann diese einfachen Funktionen zu integrieren. Hier werden nur die einfachsten Formeln angegeben, die mit einer festen Unterteilung des Integrationsintervalls in n Abschnitte arbeiten (eine Alternative dazu sind z. B. Verfahren,die mit fortgesetzter Intervallhalbierung bis zum Erreichen einer vorzugebenden Genauigkeit rechnen, wie z. B. das Romberg-Verfahren). Das Integrationsintervall wird (siehe Bild oben rechts) in n Abschnitte der Breite h = (b - a) / n unterteilt. Die so genannten Newton-Cotes-Formeln arbeiten mit den Funktionswerten an den Intervallgrenzen. Der einfachste Vertreter ist die TRAPEZREGEL I ≈ ( y0/2 + y1 + y2 + y3 + ....... + yn/2 ) h , die die Fläche unter der Kurve durch einen Polygonzug ersetzt. Weil jedes Intervall durch ein Trapez angenähert wird, ist bei einsinnig gekrümmten Funktionen der Wert für alle Abschnitte entweder zu klein oder zu groß. Eine wesentlich bessere Näherung wird erreicht, wenn durch die jeweils drei Punkte zweier benachbarter Abschnitte eine quadratische Parabel gelegt wird. In diesem Fall muss die Anzahl der Abschnitte n geradzahlig sein. Das Ergebnis dieser Näherung ist die so genannte SIMPSONSCHE REGEL: I ≈ ( y0 + 4 y1 + 2 y2 + 4 y3 + 2 y4 + 4 y5 + ....... + 2 yn-2 + 4 yn-1 + yn ) h/3 .
I ≈ ( y1 + y2 + y3 + ....... + yn ) h . Diese Formel nähert jeden Abschnitt der Fläche unter der Kurve durch ein Rechteck, dessen Höhe dem Funktionswert in der Mitte des Abschnitts entspricht. |
|||||||||||||||||||||||||||||
|
Im folgenden MATLAB-Script werden die drei oben angegebenen Formeln und zusätzlich die in MATLAB für die numerische Integration verfügbare Funktion quad demonstriert. Als (beliebig austauschbarer) Integrand wurde die sin-Funktion eingetragen, die in den (ebenfalls beliebig modifizierbaren) Grenzen von 0 ... π/2 das exakte Ergebnis 1 (Fläche unter einem Viertel der vollen sin-Schwingung) liefern würde, mit dem die numerisch gewonnenen Werte verglichen werden können. Hier wird das Integrationsintervall in n = 100 Abschnitte unterteilt, was natürlich auch beliebig geändert werden kann. |
|||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||
 |
|||||||||||||||||||||||||||||
|
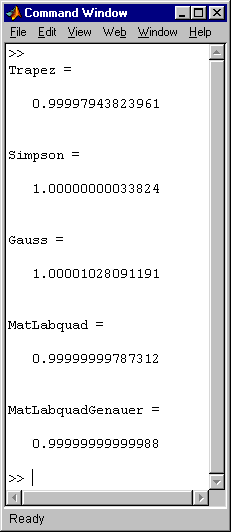
Das oben gelistete MATLAB-Script liefert im Command Window die nebenestehend zu sehenden Ergebnisse ab. Man erkennt, dass mit 100 Abschnitte recht gute Näherungen erzielt werden. Die MATLAB-Funktion quad arbeitet rekursiv bis zum Erreichen der vorgegebenen Genauigkeit. |
|||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||
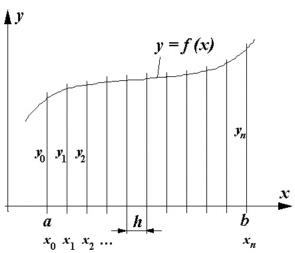 Die Formeln für die Näherung der Lösung des bestimmten Integrals
Die Formeln für die Näherung der Lösung des bestimmten Integrals
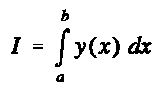
 Eine Alternative zu den NEWTON-COTES-Formeln (Trapezregel,
Simpsonsche Regel und viele andere) sind die numerischen Integrationsformeln von Gauß, die mit Funktionswerten arbeiten, die jeweils im Inneren der Intervalle liegen (die Punkte im Inneren des Intervalls liegen
dabei jeweils an den Stellen, mit denen die bestmögliche Näherung erreicht wird). Diese hinsichtlich der erreichbaren Genauigkeit im Verhältnis zum erforderlichen Aufwand optimalen Formeln haben manchmal den Nachteil,
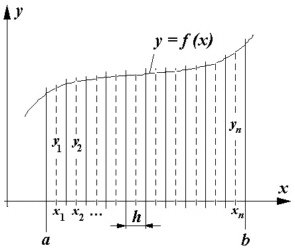
dass die für andere Berechnungen häufig ohnehin erforderlichen Werte (z. B. an den Intervallgrenzen) nicht genutzt werden. Die einfachste Formel dieser Gruppe benötigt nur die n Funktionswerte in der Mitte der Intervalle
(nebenstehende Skizze) und hat den besonders einfachen Aufbau:
Eine Alternative zu den NEWTON-COTES-Formeln (Trapezregel,
Simpsonsche Regel und viele andere) sind die numerischen Integrationsformeln von Gauß, die mit Funktionswerten arbeiten, die jeweils im Inneren der Intervalle liegen (die Punkte im Inneren des Intervalls liegen
dabei jeweils an den Stellen, mit denen die bestmögliche Näherung erreicht wird). Diese hinsichtlich der erreichbaren Genauigkeit im Verhältnis zum erforderlichen Aufwand optimalen Formeln haben manchmal den Nachteil,
dass die für andere Berechnungen häufig ohnehin erforderlichen Werte (z. B. an den Intervallgrenzen) nicht genutzt werden. Die einfachste Formel dieser Gruppe benötigt nur die n Funktionswerte in der Mitte der Intervalle
(nebenstehende Skizze) und hat den besonders einfachen Aufbau: