 |
 |
 |
|
 |
 |
 |
|
 |
 |
 |
 |
 |
 |
 |
 |
|
 |
 |
 |
|
 |
 |
 |
 |
 |
 |
|
|
 |
|
 |
|
|
|
|
|
Zu jeder symmetrischen Matrix A gehört eine so genannte “quadratische Form”
Q (x) = xT A x
mit einem (beliebigen) Spaltenvektor x und dem dazu transponierten Vektor xT. Unter der Voraussetzung, dass Q (x) für keinen (beliebigen!) Vektor x negativ wird und Q (x)
= 0 nur für den Nullvektor x = o gilt, nennt man die Matrix A “positiv definit”. Solche Matrizen sind immer auch regulär.
|
|
|
|
|
“Positiv definit”, was ist das?
|
|
|
|
|
|
|
Die nebenstehend angegebene Definition der “positiven Definitheit” mag abstrakt klingen, hat aber für die Mechanik eine wichtige praktische Bedeutung. Die kinetische Energie eines Massensystems (A enthält Massen und Massenträgheitsmomente, x die Geschwindigkeiten bzw. Winkelgeschwindigkeiten) oder die Formänderungsenergie, die in einem elastischen System gespeichert ist (A ist dann die so genannte “Steifigkeitsmatrix”) können z. B. als “quadratische Formen” formuliert werden. Da solche Energieausdrücke niemals negativ sein können, erfüllen die Matrizen, mit denen sie formuliert werden, immer die Bedingung der “positiven Definitheit”.
Das wichtigste praktische Beispiel sind die Matrizen, mit denen die (meist außerordentlich großen) Gleichungssysteme der Finite-Elemente-Methode formuliert werden.
|
|
|
|
|
|
|
|
Viel wichtiger aber ist der Umkehrschluss: Wenn z. B. in einem linearen Gleichungssystem
A x = b ,
mit dem ein elastostatisches Finite-Elemente-Modell beschrieben wird, die Matrix A nicht positiv definit ist, dann beschreibt diese Matrix kein sinnvolles mechanisches Modell. Deshalb wird in Finite-Elemente-Programmen die Definitheit immer überprüft, gegebenenfalls wird die Rechnung mit dem Hinweis “Koeffizientenmatrix ist nicht positiv definit” abgebrochen.
Noch wichtiger ist es natürlich, die Ursachen dafür zu finden und zu beseitigen. Fast immer ist eine der beiden folgenden Ursachen der Grund für diesen Fehler:
- Das System ist nicht ausreichend gelagert oder innerlich nicht tragfähig. Im Allgemeinen kann ein solches System sich “als starrer Körper bewegen” (vgl. hierzu die Beispiele aus der Statik).
- Es gibt Teile des Systems, denen keine Steifigkeitsparameter zugeordnet wurden (z. B. Elastizitätsmodul, Querschnittsflächen, Flächenträgheitsmomente, ...).
|
|
|
|
|
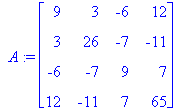 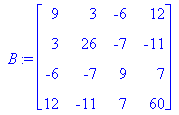 Das Überprüfen der Definitheit einer Matrix ist aufwändig (dass
z. B. die links zu sehende Matrix A positiv definit ist, die rechts zu sehende Matrix B dagegen nicht, sieht man den Matrizen nicht an). Deshalb wird folgender Weg gewählt: Für die Lösung
des Gleichungssystems wird ein Verfahren benutzt, das nur für positiv definite Matrizen funktioniert, so dass die Überprüfung auf Definitheit gewissermaßen “nebenbei erledigt” wird. Besonders beliebt ist das Verfahren
von Cholesky, bei dem im ersten Schritt die Matrix A entsprechend Das Überprüfen der Definitheit einer Matrix ist aufwändig (dass
z. B. die links zu sehende Matrix A positiv definit ist, die rechts zu sehende Matrix B dagegen nicht, sieht man den Matrizen nicht an). Deshalb wird folgender Weg gewählt: Für die Lösung
des Gleichungssystems wird ein Verfahren benutzt, das nur für positiv definite Matrizen funktioniert, so dass die Überprüfung auf Definitheit gewissermaßen “nebenbei erledigt” wird. Besonders beliebt ist das Verfahren
von Cholesky, bei dem im ersten Schritt die Matrix A entsprechend
A = RT R
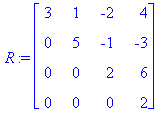 in das Produkt einer Rechtsdreiecksmatrix und ihrer Transponierten zerlegt wird. Dies ist nur
möglich, wenn A positiv definit ist. Die oben links zu sehende Matrix A lässt sich nach Cholesky zerlegen, man erhält die rechts zu sehende Rechtsdreiecksmatrix, für die die Linksmultiplikation
mit ihrer Transponierten wieder die Matrix A ergibt, für die oben rechts zu sehende Matrix B ist eine solche Zerlegung (im Bereich der reellen Zahlen) nicht möglich. in das Produkt einer Rechtsdreiecksmatrix und ihrer Transponierten zerlegt wird. Dies ist nur
möglich, wenn A positiv definit ist. Die oben links zu sehende Matrix A lässt sich nach Cholesky zerlegen, man erhält die rechts zu sehende Rechtsdreiecksmatrix, für die die Linksmultiplikation
mit ihrer Transponierten wieder die Matrix A ergibt, für die oben rechts zu sehende Matrix B ist eine solche Zerlegung (im Bereich der reellen Zahlen) nicht möglich.
|
|
|
|
Homepage
|
|
|
|
www.D@nkert.de
|
|
|
 |
|
|
|
|
|
|
 |
|
|
|
|
|
|
|
D
|
 |
|
nkert.de
|
|
|
|
|
|
|
 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|



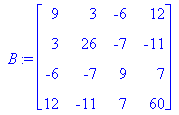 Das Überprüfen der Definitheit einer Matrix ist aufwändig (dass
z. B. die links zu sehende Matrix A positiv definit ist, die rechts zu sehende Matrix B dagegen nicht, sieht man den Matrizen nicht an). Deshalb wird folgender Weg gewählt: Für die Lösung
des Gleichungssystems wird ein Verfahren benutzt, das nur für positiv definite Matrizen funktioniert, so dass die Überprüfung auf Definitheit gewissermaßen “nebenbei erledigt” wird. Besonders beliebt ist das Verfahren
von Cholesky, bei dem im ersten Schritt die Matrix A entsprechend
Das Überprüfen der Definitheit einer Matrix ist aufwändig (dass
z. B. die links zu sehende Matrix A positiv definit ist, die rechts zu sehende Matrix B dagegen nicht, sieht man den Matrizen nicht an). Deshalb wird folgender Weg gewählt: Für die Lösung
des Gleichungssystems wird ein Verfahren benutzt, das nur für positiv definite Matrizen funktioniert, so dass die Überprüfung auf Definitheit gewissermaßen “nebenbei erledigt” wird. Besonders beliebt ist das Verfahren
von Cholesky, bei dem im ersten Schritt die Matrix A entsprechend
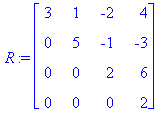 in das Produkt einer Rechtsdreiecksmatrix und ihrer Transponierten zerlegt wird. Dies ist nur
möglich, wenn A positiv definit ist. Die oben links zu sehende Matrix A lässt sich nach Cholesky zerlegen, man erhält die rechts zu sehende Rechtsdreiecksmatrix, für die die Linksmultiplikation
mit ihrer Transponierten wieder die Matrix A ergibt, für die oben rechts zu sehende Matrix B ist eine solche Zerlegung (im Bereich der reellen Zahlen) nicht möglich.
in das Produkt einer Rechtsdreiecksmatrix und ihrer Transponierten zerlegt wird. Dies ist nur
möglich, wenn A positiv definit ist. Die oben links zu sehende Matrix A lässt sich nach Cholesky zerlegen, man erhält die rechts zu sehende Rechtsdreiecksmatrix, für die die Linksmultiplikation
mit ihrer Transponierten wieder die Matrix A ergibt, für die oben rechts zu sehende Matrix B ist eine solche Zerlegung (im Bereich der reellen Zahlen) nicht möglich.