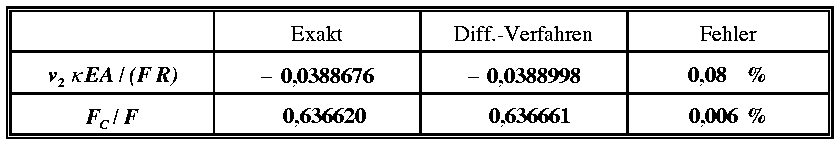Technische Mechanik, computerunterstützt, Verteiler

Ein MATLAB-Beispiel
wird hier ausführlich
beschrieben

Beispiel auf Seiten 321 und 322, Lösung mit MATLAB

MATLAB bietet zwar die Möglichkeit, mit “dünn besetzten Matrizen” (sparse matrices) zu operieren, aber für Beispiele dieser Art lohnt es sich nicht,

weil moderne PCs auch bei Gleichungssystemen mit mehreren hundert Unbekannten nur Rechenzeiten von wenigen Sekunden benötigen,
andererseits MATLAB die Definition der Matrizen mit minimalen Aufwand ermöglicht.

Die nachfolgend gelistete “M-Datei” baut das Gleichungssystem für eine Einteilung des Viertelkreises in n_A= 80 Abschnitte auf, so dass sich ein Gleichungssystem mit 125 Gleichungen ergibt (entspricht der Beschreibung auf den Seiten 321 und 322). Es ist aber so allgemein gehalten, dass durch Änderung nur dieses einen Wertes (in der hellblauen Zeilen am Anfang) eine beliebig andere Einteilung (geradzahliges n) möglich ist.

% Differenzenverfahren für Halbkreisbogen (Seiten 321 und 322)

clear all
format long ;

kappa = 0.0006258 ; % ... für r/R=0,5 aus Tabelle auf Seite 312
nA = 80 ; % Anzahl der Abschnitte, in die der Träger eingeteilt wird
n = nA*3/2+5 ; % Anzahl der Gleichungen
h = pi / (nA*2) ;

A = zeros(n,n) ; % Koeffizientenmatrix A
b = zeros(n,1) ; % Vektor der rechten Seite

% Anordnung der Unbekannten im Lösungsvektor bei nA=80 (n=125):
% [ FC v1 v2 v3 ... v83 u2 u4 u6 ... u82 ]

% v-Gleichungen:
j = 1 ;
for i=2:nA+2
   phi = (i-2)*h ;
   A(j,1) = h*h*cos(phi) ; % Erste Spalte
   A(j,j+1:j+3) = [1 h*h-2 1] ;
   b(j,1) = h*h*(1-sin(phi)) ;
   j = j + 1 ;
end

% u-Gleichungen:
k = nA+5 ;
for i=3:2:nA+1
   A(j,k:k+1) = [-1 1] ;
   A(j,i+1) = 2*h ;
   b(j,1) = -2*h*kappa ;
   j = j + 1 ;
   k = k + 1 ;
end

% Randbedingungen:
A(j,2) = -1 ;
A(j,4) = 1 ;
j = j + 1 ;
A(j,nA+5) = 1 ;
j = j + 1 ;
A(j,n) = 1 ;
j = j + 1 ;
A(j,nA+3) = 1 ;

x = A \ b ;

clf ;

% Graphische Darstellung des unverformten Halbkreises (angenommener Radius: 1) und
% des verformten Halbkreises, Verformungen werden mit einem Faktor so vergrößert,
% dass die maximale Absenkung (unter der Kraft) einem Viertel des Radius entspricht:
Radius = 1 ;
faktor = Radius / (-x(3)*4) ;

for i=0:nA/2
   % Koordinaten des unverformten Halbkreises:
   kx(i+1) = -Radius*cos(i*2*h) ;
   kx(nA-i+1) = -kx(i+1) ;
   ky(i+1) = Radius*sin(i*2*h) ;
   ky(nA-i+1) = ky(i+1) ;
   % Koordinaten des verformten Halbkreises:
   vx(i+1) = (Radius+x(nA+3-i*2)*faktor) * kx(i+1) - x(n-i) * faktor * ky(i+1) ;
   vx(nA-i+1) = -vx(i+1) ;
   vy(i+1) = (Radius+x(nA+3-i*2)*faktor) * ky(i+1) + x(n-i) * faktor * kx(i+1) ;
   vy(nA-i+1) = vy(i+1) ;
end

plotyy (kx,ky,vx,vy)

Ergebnisv2 = x(3)
ErgebnisFc = x(1)

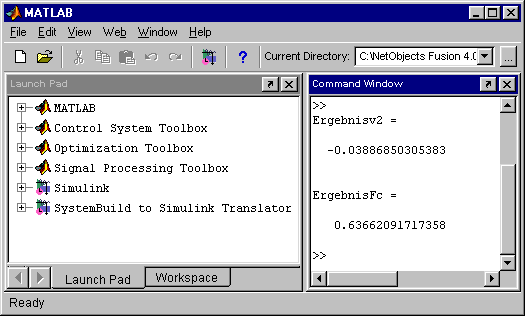
Die drei weißen Zeilen am Ende sorgen für die Ausgabe der Ergebnisse. In das “Command Window” werden die beiden Werte (Absenkung des Kraftangriffspunktes, und “Statisch Unbestimmte” F_C) ausgegeben, die auf der Seiten 322 mit den exakten Werten verglichen werden:

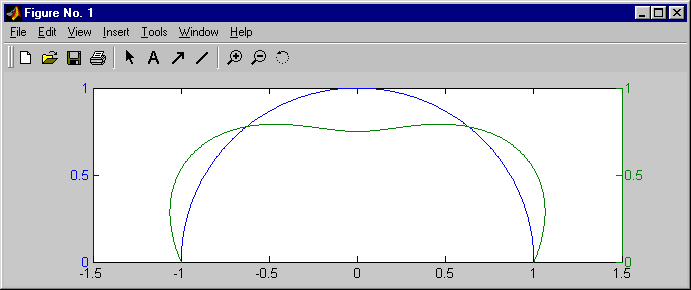
Mit der Funktion plotyy werden zwei Funktionen in ein Graphik-Fenster ausgegeben, der unverformte Halbkreis und der verformte Träger, wobei die Verschiebungen (vgl. Kommentar in der oben gelisteten Datei) stark vergrößert wurden:

Die Ergebnisse in der Tabelle auf Seite 322

werden durch die Rechnung bestätigt. Die ohnehin beeidruckende Genauigkeit des Differenzenverfahrens kann bei feinerer Unterteilung durchaus noch gesteigert werden. Eine Einteilung des Viertelkreises in 480 Abschnitte z. B. (das Gleichungssystem hat dann 725 Gleichungen) kann durch die Änderung einer Zeile realisiert werden:

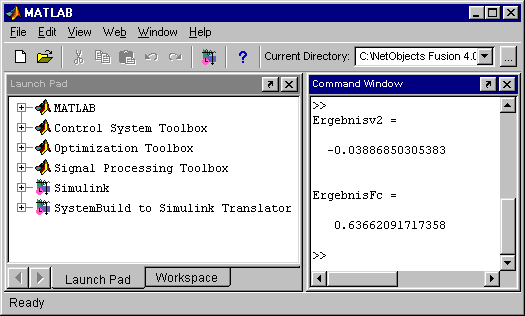
Im “Command Window” sieht man folgende Ergebnisse:

Die oben gelistete M-Datei ist als S322.m zum Download verfügbar.

Homepage

www.D@nkert.de

nkert.de