|
Elementsteifigkeitsmatrix
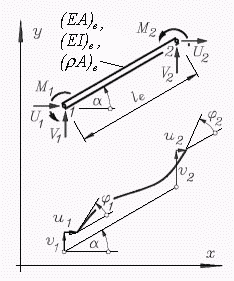
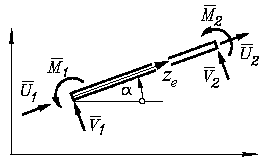 Es soll die Elementssteifigkeitsmatrix für das 6-Freiheitsgrade-Rahmenelement für den Sonderfall "Konstante Parameter EI, EA" entwickelt werden. Zunächst wird auf der Basis der allgemeinen Formel gearbeitet, die sich auf die elementeigenen Richtungen (das "Querstrich-System", siehe nebenstehende Skizze) bezieht. Es soll die Elementssteifigkeitsmatrix für das 6-Freiheitsgrade-Rahmenelement für den Sonderfall "Konstante Parameter EI, EA" entwickelt werden. Zunächst wird auf der Basis der allgemeinen Formel gearbeitet, die sich auf die elementeigenen Richtungen (das "Querstrich-System", siehe nebenstehende Skizze) bezieht.
In der für diese Belastungs- und Verformungsrichtungen geltenden Formel für die Elementsteifigkeitsmatrix
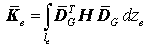
mit
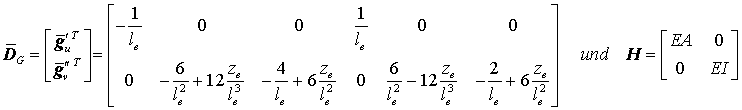
werden zunächst die Matrizen unter dem Integral ausmultipliziert. Danach können alle Elemente der so entstandenen symmetrischen Matrix mit 6 Zeilen und 6 Spalten geschlossen integriert werden (das geht nur wegen der Annahme konstanter Werte für EI und EA) . Man erhält:
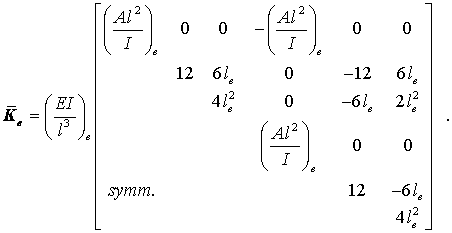
 Diese Formel findet man auch in "Dankert/Dankert: Technische Mechanik" auf Seite 279, wo sie allerdings auf ganz anderem Wege hergeleitet wurde. Die Transformation auf die globalen Richtungen entsprechend Diese Formel findet man auch in "Dankert/Dankert: Technische Mechanik" auf Seite 279, wo sie allerdings auf ganz anderem Wege hergeleitet wurde. Die Transformation auf die globalen Richtungen entsprechend
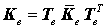
mit der Transformationsmatrix
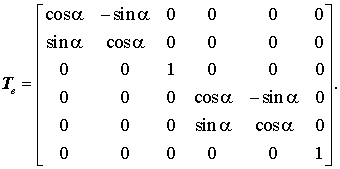
kann auch noch "von Hand" erledigt werden, und man erhält schließlich die Elementsteifigkeitsmatrix des ebenen Rahmenelements mit konstanter Biegesteifigkeit und konstanter Dehnsteifigkeit:
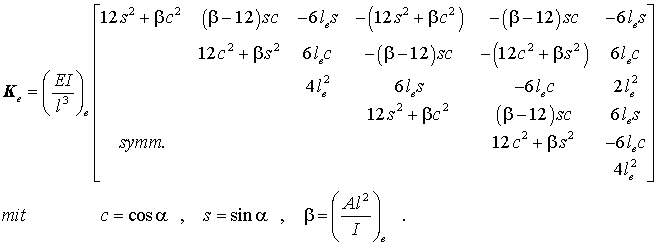
Auch diese Matrix findet man in "Dankert/Dankert: Technische Mechanik" (Seite 281), hergeleitet auf einer anderen Basis.
|

