|
Für den Vergleich mit den exakten Werten können einzelne Werte z. B. nach dem Satz von Castigliano oder mit dem Einheitslastverfahren auf der Basis der Arbeitsgleichung berechnet werden. Effektiver ist aber die Nutzung eines FEM-Programms, das für diesen Fall auch die (im Sinne der klassischen Biegetheorie) exakte Lösung liefert. Diese Lösung findet man hier. Aber es ist durchaus auch noch möglich, für diese Aufgabe die Biegeverformung v(z) durch Integration der Differenzialgleichung der Biegelinie zu ermitteln. Nach etwas mühsamer Rechnung erhält man:
Der Biegemomentenverlauf ist proportional zur 2. Ableitung der Biegelinie:
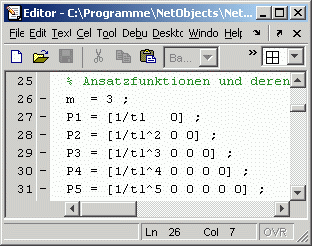
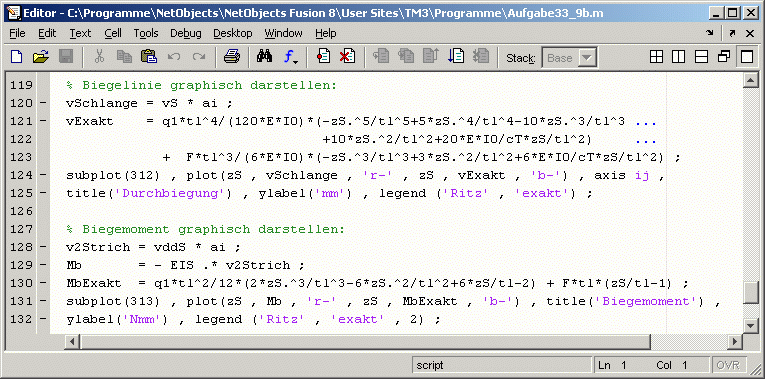
Diese beiden Funktionen werden verwendet, um den Vergleich mit der Näherungslösung nach dem Ritzschen Verfahren durchzuführen. Die Lösung mit Matlab wird mit einer Modifikation des Scripts, das für die Aufgabenstellung a verwendet wurde, realisiert. Darin wird nur die graphische Ausgabe der Biegelinie und des Momentenverlaufs erweitert um die Darstellung der oben zu sehenden Funktionen der exakten Lösung. Dieser Bereich des Scripts sieht dann so aus:
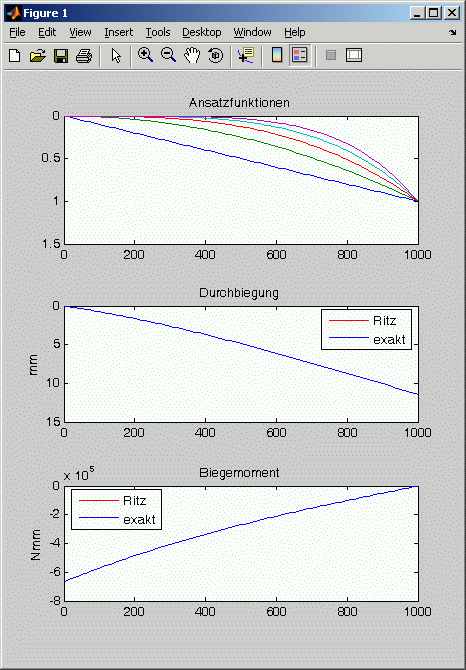
Bei den Biegemomenten ist die Übereinstimmung nicht so gut (vgl. auch den Zahlenwert für das Biegemoment am rechten Rand bei der Aufgabenstellung a, dort darf eigentlich kein Biegemoment sein). Das liegt daran, dass das Biegemoment proportional zur 2. Ableitung der Verschiebung ist und bei einem Verschiebungsansatz mit maximal 3. Potenz in den Funktionen kann das Biegemoment nur durch eine Gerade genähert werden. Man sieht in der Graphik sehr schön, wie diese Gerade versucht, die exakte Lösung (Polynom 3. Grades) bestmöglich zu nähern. Bei Verwendung von mehr Ansatzfunktionen wird die Näherung auch des Biegemomentenverlaufs sehr schnell besser. Das für die Aufgabenstellung a entwickelte Script ist vorbereitet für die Rechnung mit maximal 5 Ansatzfunktionen. In der Zeile 26 muss nur der Wert für m auf 4 bzw. 5 erhöht werden, um mit 4 bzw. 5 Ansatzfunktionen zu rechnen: Nachfolgend sieht man die Graphiken für die Rechnung mit 4 Ansatzfunktionen (linkes Bild) bzw. 5 Ansatzfunktionen (rechtes Bild). Während man bei 4 Ansatzfunktionen gerade noch erkennen kann, dass in den Fenstern jeweils 2 Kurven dargestellt werden, überdecken sich die Kurven bei 5 Ansatzfunktionen total (man vergleiche auch die Zusammenstellung der Zahlenwerte an markanten Punkten auf der Seite mit der Aufgabenstellung).
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||


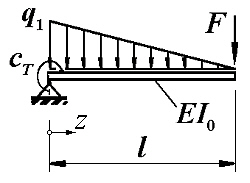 Der skizzierte Biegeträger mit konstanter Biegesteifigkeit ist am linken Rand in einem
Festlager gelagert und durch eine Drehfeder gefesselt.
Der skizzierte Biegeträger mit konstanter Biegesteifigkeit ist am linken Rand in einem
Festlager gelagert und durch eine Drehfeder gefesselt.
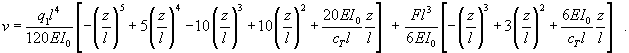
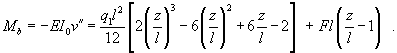
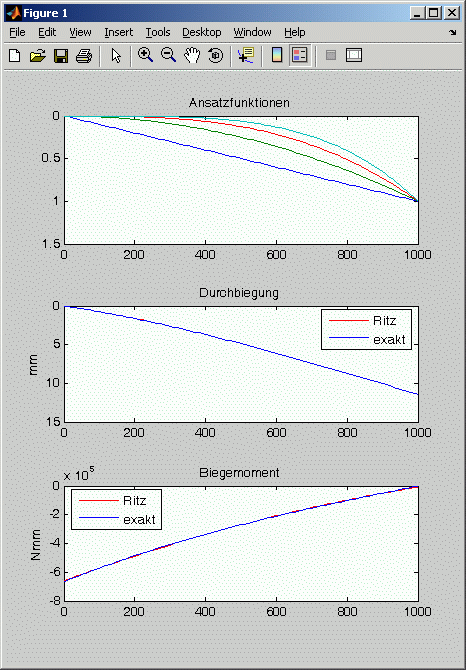
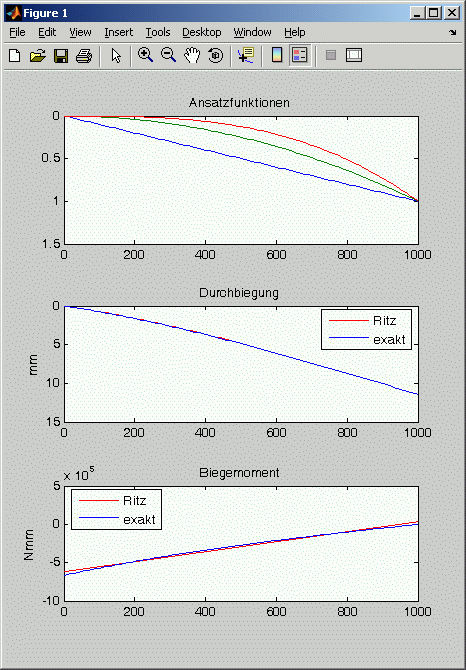 Das nebenstehend zu sehende Ergebnis der Rechnung (mit 3 Ansatzfunktionen) zeigt, dass die Verschiebung schon mit wenigen
Ansatzfunktionen durch das Ritzsche Verfahren ausgezeichnet genähert wird (die Näherungslösung und die exakte Lösung überdecken sich fast komplett).
Das nebenstehend zu sehende Ergebnis der Rechnung (mit 3 Ansatzfunktionen) zeigt, dass die Verschiebung schon mit wenigen
Ansatzfunktionen durch das Ritzsche Verfahren ausgezeichnet genähert wird (die Näherungslösung und die exakte Lösung überdecken sich fast komplett).