|
Bei dynamischen Problemen bietet sich das Hamiltonsche Prinzip
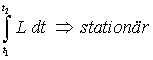
als Ausgangspunkt an: Zwischen zwei Zeitpunkten t1 und t2 verläuft die Bewegung eines Massensystems so, dass das Zeitintegral über die (für konservative Systeme geltende) Lagrangesche Funktion
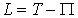
einen stationären Wert annimmt. Π ist das elastische Potential, T die kinetische Energie des Systems, die für ein einzelnes finites Element in der Form
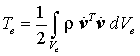
aufgeschrieben werden kann mit
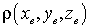 - Dichte des Materials (ist in der Regel konstant), - Dichte des Materials (ist in der Regel konstant),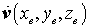 - Geschwindigkeitsfeld der Massenpunkte. - Geschwindigkeitsfeld der Massenpunkte.
Für das Geschwindigkeitsfeld wird die gleiche Strategie gewählt, mit der im elastostatischen Fall die Verschiebungen durch die Knotenverschiebungen ausgedrückt wurden:
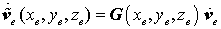
stellt den Zusammenhang der Knotengeschwindigkeiten mit dem Geschwindigkeitsfeld im Inneren des Elements mit den gleichen Ansatzfunktionen her, die auch für den elastostatischen Fall verwendet (und wie dort erzeugt) werden. Damit ergibt sich der Integralausdruck für die kinetische Energie in einem Element zu
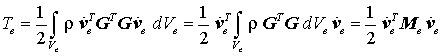
(die Knotengeschwindigkeitsvektoren können aus dem Integral herausgezogen werden) mit der so genannten Elementmassenmatrix
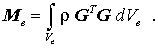
Damit kann die Lagrangesche Funktion für ein finites Element aus kinetischer Energie und elastischem Potential zusammengesetzt werden:
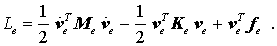
Zum Hamiltonschen Prinzip gehören die “Lagrangeschen Gleichungen 2. Art” (vgl. Abschnitt 33.4.3 auf Seite 633)
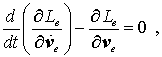
die mit der Lagrangeschen Funktion für ein Element auf folgendes Differenzialgleichungssystem führt:
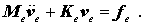
Hierin sind Ke und fe die Elementsteifigkeitsmatrix und der Elementbelastungsvektor wie für das elastostatische Problem, Me ist die Elementmassenmatrix, für die die gerade entwickelte Formel gilt.
Auch hier sind die Überlegungen zunächst für ein Element angestellt worden. Das Zusammensetzen der Elementmassenmatrizen zur Systemmassenmatrix erfolgt nach dem gleichen “Einspeicherungs-Algorithmus” wie für die Steifigkeitsmatrizen. An den Knoten zusätzlich vorhandene diskrete Massen dürfen auf die entsprechenden Hauptdiagonalelemente der Systemmassenmatrix addiert werden.
Im Gegensatz zum elastostatischen Problem entsteht bei dynamischen Problemen ein Differenzialgleichungssystem
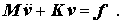
Wenn z. B. die freien Schwingungen (f = o) berechnet werden sollen, führt der aus der Schwingungslehre bekannte Ansatz (vgl. Kapitel 32 auf Seite 603)
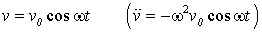
auf das allgemeine symmetrische Matrizeneigenwertproblem
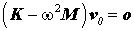
das die Eigenkreisfrequenzen der Schwingung ω und die zugehörigen Eigenschwingungsformen liefert.
|





