Idee des Cholesky-Verfahrens

Für den wichtigen Spezialfall eines linearen Gleichungssystems mit symmetrischer Koeffizientenmatrix lässt sich der verkettete Algorithmus derart abwandeln, das die Anzahl der erforderlichen Operationen auf etwa die Hälfte verringert wird. Eine als Verfahren von Cholesky bezeichnete Modifikation hat aus verschiedenen Gründen besondere Bedeutung erlangt. Hierbei wird die symmetrische Matrix A des Systems

entsprechend

in ein Produkt zweier zueinander transponierter Dreiecksmatrizen zerlegt. Die Ermittlung des Vektors der Unbekannten x aus

kann dann wie beim verketteten Algorithmus durch Vorwärtseinsetzen

und Rückwärtseinsetzen

realisiert werden.

Cholesky-Zerlegung

Nebenstehend ist das Falksche Schema für die Rückmultiplikation zu sehen, das den erforderlichen Algorithmus für die Gewinnung von R verdeutlicht (zur Erinnerung: Jedes Element a_ij der Matrix A muss sich aus dem Skalarprodukt der i-ten Zeile von R^T mit der j-ten Spalte von R ergeben):

• Das Skalarprodukt aus der ersten Zeile von R^T mit der ersten Spalte von R ist besonders einfach:

• Das Skalarprodukt aus der ersten Zeile von R^T mit einer beliebigen anderen Spalte von R enthält mit nunmehr bekanntem r₁₁ jeweils nur ein unbekanntes Element r_1j von R, so dass die erste Zeile von R berechnet werden kann .
   
• Das Skalarprodukt aus der zweiten Zeile von R^T mit der zweiten Spalte von R enthält neben dem inzwischen bekannten r₁₂ nur das unbekannte r₂₂, das wie die Berechnung aller Hauptdiagonalelemente das Ziehen einer Quadratwurzel erfordert.
   
• Man setzt dieses Spiel nun mit den Skalarprodukten der zweiten Zeile von R^T und allen Spalten von R fort, danach mit der dritten Zeile von R^T usw. Der mit dem Falkschen Schema veranschaulichte Prozess kann durch eine Formel ausgedrückt werden:

• Für die Berechnung der Hauptdiagonalelemente von R (in der Formel steht auf der linken Seite r_ii·r_ii muss die Quadratwurzel gezogen werden. Bei positiv definiter Matrix entstehen dabei nur reelle (positive) Elemente, anderenfalls können die r_ii und damit alle Elemente dieser Zeile rein imaginär werden.

Einfaches Beispiel

Es soll das folgende lineare Gleichungssystem mit symmetrischer Koeffizientenmatrix nach dem Verfahren von Cholesky gelöst werden:

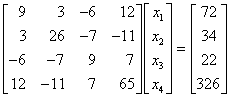
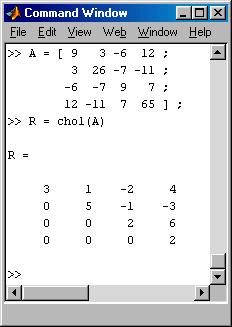
Zunächst wird die Cholesky-Zerlegung der Matrix A durchgeführt (im Bildschirm-Schnappschuss des Command Windows rechts ist die Kontrollrechnung mit der chol-function von Matlab zu sehen).

Das nachfolgend links zu sehende Falksche Schema ist so zu füllen, dass die Multiplikation der beiden zueinander transponierten Dreiecksmatrizen die eingetragene Matrix A ergibt:

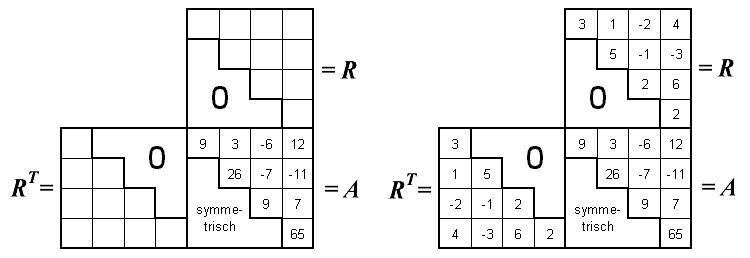
Rechts sieht man das ausgefüllte Schema. Als erster Wert entsteht die 3 (links oben), weil sich bei Multiplikation der ersten Zeile von R^T mit der ersten Spalte von R die auf der Position links oben in A stehende 9 ergeben muss. Dann geht es wie oben beschrieben weiter, wobei man stets die in R entstehenden Elemente auch nach R^T übertragen muss.

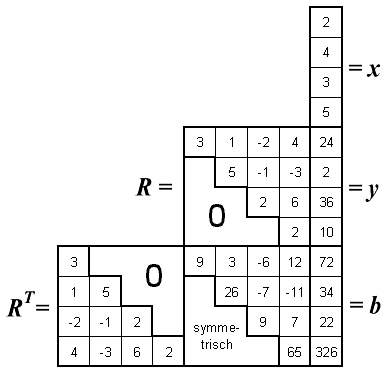Wie beim verketteten Algorithmus gestattet auch hier das Falksche Schema die kompakte Anordnung aller Matrizen und Vektoren, die bei der Cholesky-Zerlegung und dem Vorwärts- und Rückwärtseinsetzen benötigt bzw. erzeugt werden.

Nebenstehend ist das komplette Schema zu sehen. Nach der Cholesky-Zerlegung der Matrix A wird zunächst das Vorwärtseinsetzen durchgeführt, mit dem der Vektor y erzeugt wird. Es beginnt damit, dass die Multiplikation der ersten Zeile von R^T mit y eine 72 ergeben muss, also 3·y₁=72, so dass als y₁ die 24 eingetragen werden kann. Die nächste Rechnung lautet dann (zweite Zeile von R^T mit y multipliziert): 1·24+5·y₂=34, so dass für y₂ die 2 eingetragen werden kann usw.

Analog dazu verläuft das Rückwärtseinsetzen mit der Matrix R zur Bestimmung des Vektors x, nur dass es hier mit der letzten Zeile beginnt: Multiplikation der vierten Zeile von R mit dem Vektor x führt auf die Rechnung 2·x₄=10, so dass für x₄ die 5 eingetragen werden kann usw.

Vorteile des Cholesky-Verfahrens

Die wesentlichen Vorzüge des Cholesky-Verfahrens, das neben dem Problem der Lösung linearer Gleichungssysteme auch noch in anderen Bereichen der Numerik symmetrischer Matrizen eine wichtige Rolle spielt (z. B. bei Matrizeneigenwertproblemen), sind:

• Das Verfahren arbeitet numerisch sehr stabil. Wesentlicher Grund dafür ist das Ziehen der Quadratwurzel beim Berechnen der Hauptdiagonalelemente. Dabei werden die wesentlichen Ziffern (ob von sehr großen oder sehr kleinen Zahlen ausgehend) näher an das Komma herangezogen, was in jedem Schritt einer Normalisierung ähnelt. Auf eine Pivotisierung wie beim klassischen Gauß-Verfahren oder dem verketteten Algorithmus kann verzichtet werden.
   
• Die Matrix A wird auf Definitheit geprüft (nur positiv definite Matrizen garantieren reelle Zahlen bei der Cholesky-Zerlegung). Dies sieht nur scheinbar wie eine Einschränkung der Anwendbarkeit des Verfahrens aus, denn fast alle symmetrischen Matrizen bei der Lösung von naturwissenschaftlich-technischen Problemen haben die Eigenschaft der positiven Definitheit. So wird bei der Cholesky-Zerlegung die Ausgangsmatrix selbst auf Korrektheit geprüft (man darf davon ausgehen, dass fehlerhafte Lösungen eines Problems, das auf ein lineares Gleichungssystem führt, fast ausschließlich auf falsch formulierte Gleichungssysteme zurückzuführen sind, was in der Praxis schwer zu entdecken ist).
   
• Das Verfahren eignet sich vorzüglich für die Programmierung. Wie man an dem einfachen Beispiel oben nachvollziehen kann, wird das Element a_ij bei der Berechnung von r_ij letztmalig gebraucht, so dass A von R überschrieben werden kann (minimaler Speicherbedarf). Diese Eigenschaft besitzen allerdings der klassische Gauß-Algorithmus und der verkettete Algorithmus auch.
   
• Eine bei A vorhandene Bandstruktur überträgt sich auf R (minimaler Speicherbedarf und die Möglichkeit drastischer Reduzierung des Aufwands). Dies wird vor allem bei den enorm großen Matrizen bei Finite-ElementeBerechnungen genutzt.
   
• Die Determinante der Matrix A fällt gewissermaßen nebenbei an. Nach den Regeln für die Berechnung des Wertes der Determinante eines Matrizenprodukts und dem Laplaceschen Entwicklungssatz ergibt sich die Formel:

det (A) = det (R^T) · det (R) = ( r₁₁ · r₂₂ · r₃₃ · .... · r_nn)².  .

Homepage “Dankert/Dankert: Technische Mechanik”

Homepage “WWW - Ergänzung - Vertiefung - WWW”

D

nkert.de