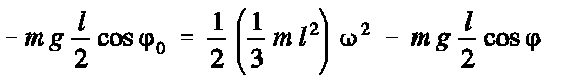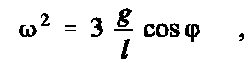Beispiel 1 auf Seiten 528/529, Lösung mit CAMMPUS

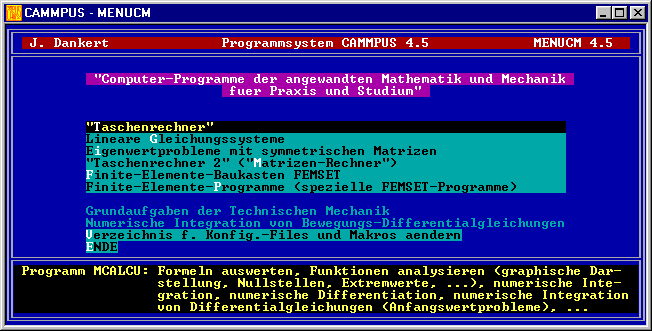
CAMMPUS starten und “Taschenrechner” wählen:

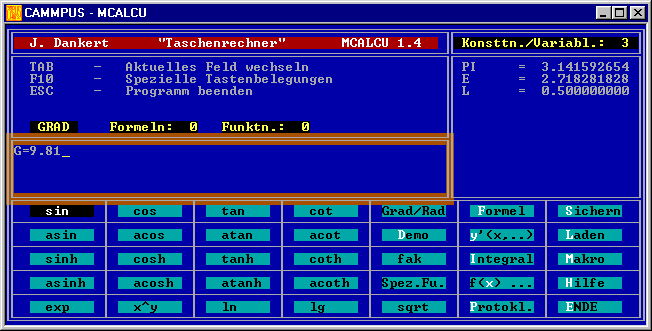
Es ist zu empfehlen, die gegebenen Werte für die Länge l und die Erdbeschleunigung g als Konstanten einzugeben, um in den Differenzialgleichungen keine Zahlenwerte verwenden zu müssen:

L = 0.5     
G = 9.81

Der nachfolgende Bildschirm-Schnappschuss zeigt den Startbildschirm des “Taschenrechners” mit dem bereits im Konsttn./Variabln.-Speicher zu sehenden Wert für L unmittelbar vor dem Betätigen der Eingabetaste für die Definition der Konstanten G:  

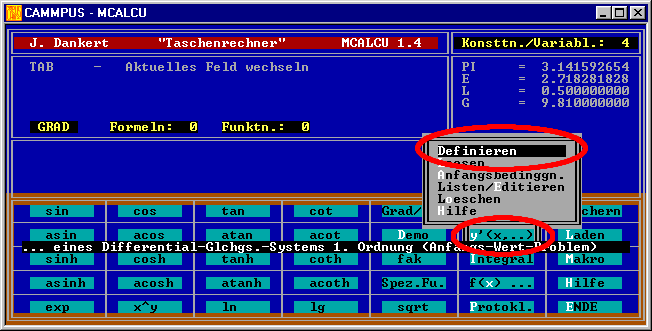
Im “Tastaturmenü” wird (am einfachsten mit der Maus) erst y’(x,..)  und im sich öffnenden Submenü Definieren  gewählt:

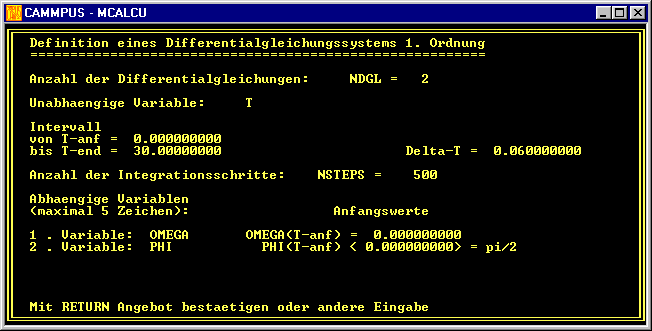
Es erscheint die Eingabemaske für die Definition des Anfangswertproblems, die wie nachfolgend zu sehen ausgefüllt wird:

Für die Anzahl der Differenzialgleichungen wurde NDGL = 2 eingegeben, der Name der unabhängigen Variablen wurde auf T geändert, als Integrationsintervall wurde 0 ... 30 gewählt, für NSTEPS (Anzahl der Integrationsschritte) wurde der voreingestellte Wert 500 bestätigt. Die Angebote für die abhängigen Variablen (Y1 bzw. Y2) wurden abgelehnt, die abhängigen Variablen heißen nun OMEGA bzw. PHI, als Anfangswerte wurden 0 (für OMEGA) bzw. π / 2 (Anfangsauslenkung) eingegeben.

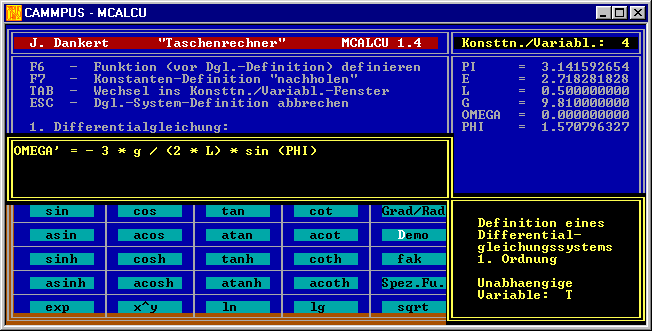
Nach Bestätigung der eingegebenen Werte werden die Differenzialgleichungen über das Eingabefeld abgefordert, wie es der folgende Bildschirm-Schnappschuss (unmittelbar vor der Eingabe der ersten Differentialgleichung) zeigt.

Wenn die Werte für g und l (Erdbeschleunigung bzw. Pendellänge) nicht bereits als Konstanten definiert wären, könnte man es nachholen (man beachte das Angebot, "vergessene" Konstanten-Definitionen nachzuholen).

Nach Eingabe der ersten Differenzialgleichung wird automatisch die zweite mit PHI’ = abgefragt. Man gibt PHI’ = OMEGA ein, und das Anfangswertproblem ist definiert.

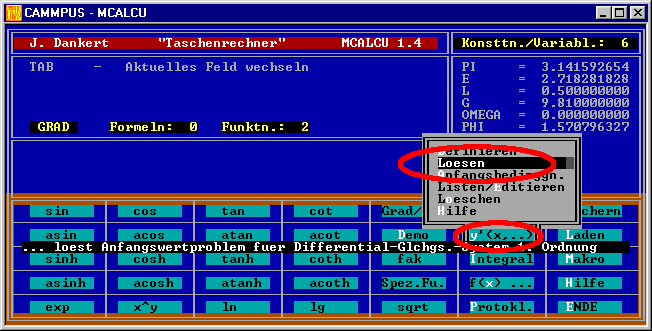
Nach der Definition des Anfangswertproblems kann im Angebot y’(x,..) die Submenü­Option Loesen angenommen werden:

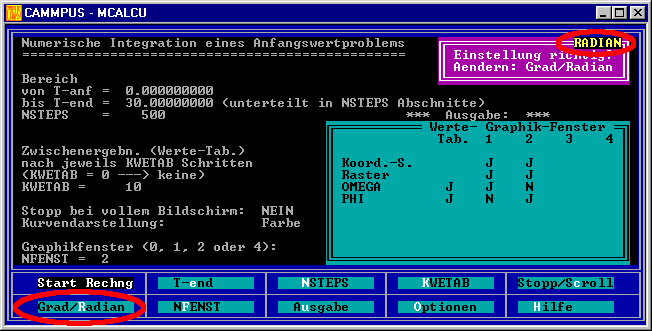
Es erscheint die nachfolgend zu sehende Maske, die die Korrektur einiger Eingabewerte und Einstellungen (z. B. die Anzahl der Integrationsschritte NSTEPS oder die Interpretation der Winkelfunktionen, die in diesem Fall unbedingt auf RADIAN eingestellt werden muss) und die Korrektur der voreingestellten Ausgabe-Strategie gestattet.

In diesem Fall wird angeboten, PHI und OMEGA als Wertetabelle auszugeben (nur jeder zehnte Wert, Voreinstellung für KWETAB, kann auch geändert werden) und in zwei Graphik-Fenstern PHI(T) bzw. OMEGA(T) zu zeichnen. Diese Voreinstellungen können akzeptiert werden, weil nach der Berechnung (im "Letzte-Chance-Menü") noch einmal eine spezielle Bildschirm-Darstellung definiert werden kann.

Nach "Start Rechnung" ...

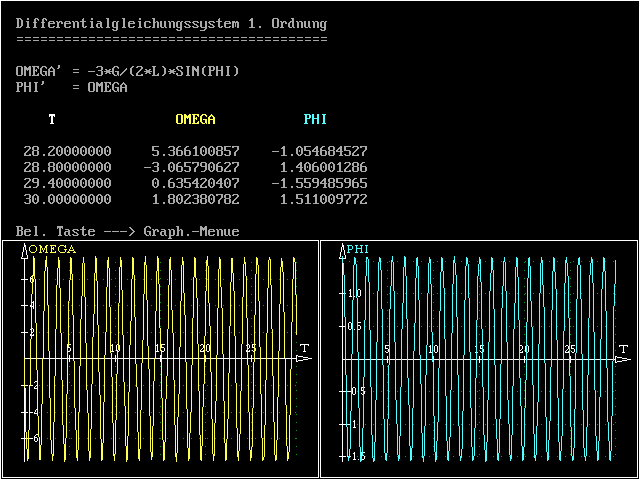
... werden simultan die Wertetabelle geschrieben und die Funktionen gezeichnet:

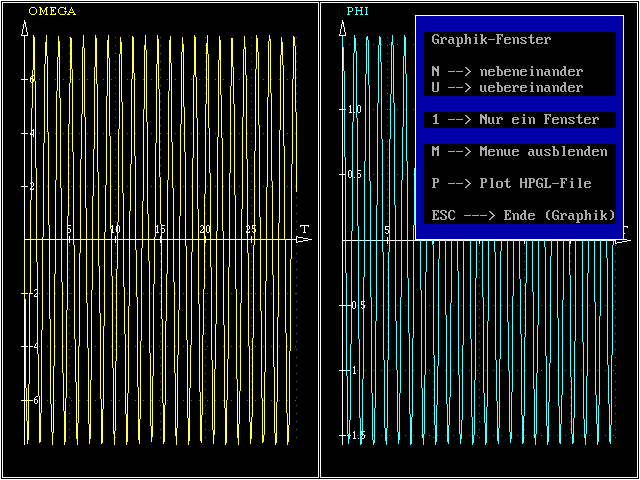
Wenn die Rechnung komplett ist, wird (nach Drücken einer beliebigen Taste) die Größe der Graphik-Fenster automatisch an die berechneten Werte angepasst, und ein Graphik-Menü bietet mehrere nützliche Optionen zur Betrachtung der Funktionen (Zoom, einzelnes Fenster bildschirmfüllend, . . . ):

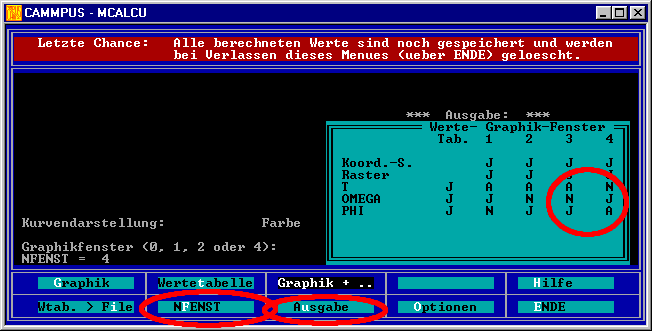
Nach dem Verlassen des Graphik-Menüs erscheint folgende Maske, ...

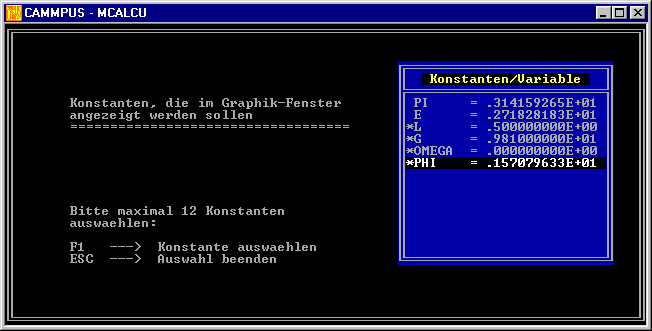
... in der schon folgende Modifikationen vorgenommen wurden: Die Anzahl der Graphik-Fenster NFENST wurde auf 4 erhöht, über das Angebot “Ausgabe”wurde für das Graphik-Fenster 3 eine weitere Darstellung PHI(T) eingestellt, im Graphik-Fenster 4 ist für die Darstellung von OMEGA die unabhängige Variable (Abszissenachse) auf PHI eingestellt worden, deshalb wird dort OMEGA(PHI) gezeichnet werden (Darstellung in der Phasenebene). Über das Menüangebot "Graphik + .." kommt man in folgendes Fenster:

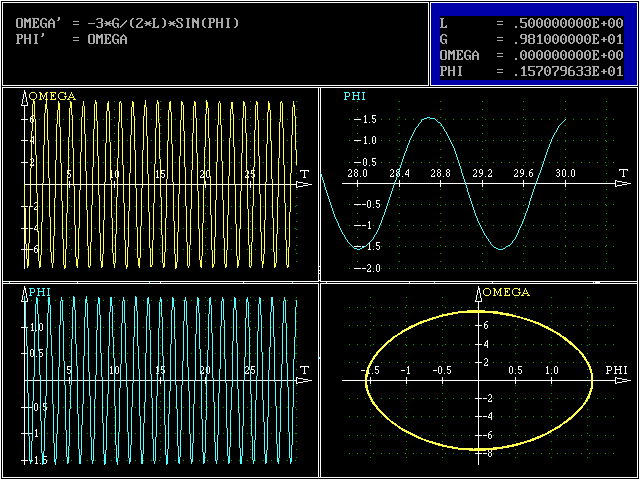
Hier wurden bereits folgende Änderungen vorgenommen: Mit der F1-Taste wurden die beiden Parameter L und G und die Anfangswerte der Variablen OMEGA und PHI ausgewählt (wird durch den vorgestellten Stern angezeigt), so dass man im Graphik-Fenster, das sich nach Drücken von ESC öffnet, im oberen Teil neben den Differenzialgleichungen sämtliche Parameter der behandelten Aufgabenstellung sieht:

In dieser Darstellung wurde vorab über das (hier ausgeblendete) Menü die Darstellung im rechten oberen Graphik-Fenster mit Hilfe der Option “Zoom” so eingestellt, dass man etwas mehr als eine volle Schwingung am Ende des berechneten Zeitintervalls sieht, was für die nachfolgend diskutierte Verifizierung der Ergebnisse nützlich ist.

Verifizierung der Ergebnisse:

An diesem Bespiel lassen sich sehr schön einige Möglichkeiten der Verifizierung der Ergebnisse diskutieren:

1. Die Rechnung wurde mit den Parametern  g = 9,81 m/s² und  l = 0,5 m ausgeführt, so dass die Zeitachse die Dimension s (Sekunde) hat. Es ist zu erkennen, daß nach 30 s (und immerhin mehr als 20 vollen Schwingungen) keine Änderungen der Amplitude in der graphischen Darstellung sichtbar sind, was besonders in der Zoom-Darstellung für das Ende des Integrationsbereichs und in der Phasenebene (die beiden Fenster rechts) deutlich wird, so dass die Rechnung als nummerisch "gesund" angesehen werden darf.
    
2. Neben dieser "physikalischen Kontrolle" sollte stets eine Kontrollrechnung mit feinerer Einteilung des Integrationsintervalls die "nummerische Gesundheit" der Rechnung bestätigen, am Ende der Kontrollmöglichkeit 3. wird diese durchgeführt.
    
3. Die sicherste Kontrolle für die Richtigkeit von Rechnungen mit physikalisch-technischen Problemen ist die Überprüfung der Einhaltung eines physikalischen Gesetzes, das nicht zur Formulierung der Aufgabe genutzt wurde, siehe 1.: Amplituden müssen für die ungedämpfte Schwingung konstant sein. Der Energiesatz gestattet sogar noch eine schärfere Kontrolle:
4. Während das Weg-Zeit-Gesetz und das Geschwindigkeits-Zeit-Gesetz für das Pendel mit großen Ausschlägen nur durch die Lösung der behandelten nichtlinearen Differenzialgleichung gefunden werden können, ist das Geschwindigkeits-Weg-Gesetz mit Hilfe des Energiesatzes leicht zu formulieren. Damit ist ein Zusammenhang zwischen den beiden berechneten Größen gegeben. Zu jedem Zeitpunkt muß nach dem Energiesatz gelten: (Null-Potential in Höhe des Aufhängepunktes A, in der Klammer auf der rechten Seite das Massenträgheitsmoment des dünnen Stabes bezüglich A). Für die Anfangsauslenkung φ₀ = π/2 vereinfacht sich dies zu der Beziehung die für jedes berechnete Wertepaar gelten muß.
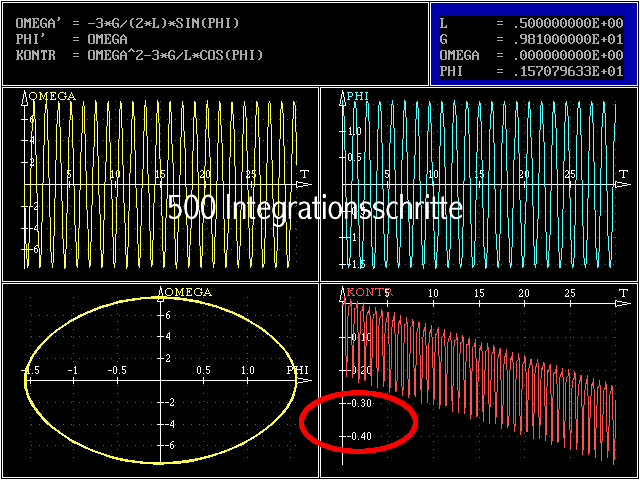
5. Besonders effektiv wird die Kontrolle, wenn man eine entsprechende Kontrollfunktion zusätzlich berecchnet. Der nachfolgende Bildschirm-Schnappschuss zeigt eine Rechnung, bei der eine entsprechend
6. KONTR = OMEGA^2 - 3 * G / L * cos (PHI)
7. definierte Funktion im unteren rechten Fenster dargestellt wird:

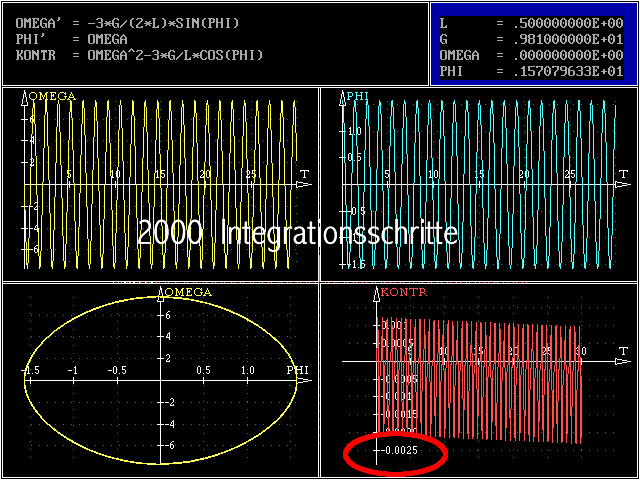
Die Größenordnung der Funktionswerte der Kontrollfunktion, die theoretisch Null sein müssten, zeigt, dass die Rechnung mit 500 Integrationsschritten doch nicht ganz so “gesund” ist, wie nach der graphischen Kontrolle unter 1. zu vermuten war (sehr deutlich sieht man auch, dass der Fehler mit fortlaufender Rechnung immer größer wird). Es wird deshalb noch eine Rechnung mit 2000 Integrationsschritten durchgeführt:

Bei 2000 Integrationsschritten liegen die Werte der Kontrollfunktion in einer Größenordnung, die der numerischen Rechnung praktisch Exaktheit bescheinigt.