 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
|
 |
 |
 |
 |
 |
|
 |
 |
 |
|
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
|
|
 |
|
|
|
 |
|
|
|
|
|
|
|
|
|
 |
|
|
|
Die nachfolgend gelistete “.m-Datei” ist zum Download verfügbar
. Es wird der Fall λ = 2 behandelt.
Für alle, die irgendeine Programmiersprache beherrschen (“kennen” dürfte eigentlich ausreichend sein), ist diese Datei weitgehend selbsterklärend, alle offenen Fragen werden sicher von der Hilfe-Funktion
von MATLAB beantwortet.
|
|
|
|
|
% 18 Computer-Verfahren für Biegeprobleme S.265
% 18.1 Das Differenzenverfahren
% 18.1.2 Biegelinie bei konstanter Biegesteifigkeit
% Beispiel 2
% MATLAB 6.0 R12
% Author: Corinna Winter
% Rev.: Dr. Thomas Frischgesell
% Datum: 24.4.03
clear all
LL = 1; % Länge
q1 = 1; % Streckenlast
EI = 1; % Biegesteifigkeit
lambda = 2;
F = lambda*q1*LL; % Kraft
nA =100; % Anzahl der Abschnitte in die der Träger eingeteilt wird
k=nA+5; % Knotenanzahl
deltax = LL/nA; % Elementlänge
A=zeros(k,k); % Erstellung einer Matrix A gefüllt mit Nullen
A(1:2,1:5) =[0 0 1 0 0 ; ...
0 -1 0 1 0]; % Randbedingung: Einspannung links
A(k-1:k,k-4:k)=[0 0 1 0 0 ; ...
0 1 -2 1 0]; % Randbedingung: Lager rechts
for i=3:k-2 % Beschreibung der Matrix A in einer Schleife mit
A(i,i-2:i+2)=[1 -4 6 -4 1]; % dem wiederkehrenden Teilstück 1 -4 6 -4 1
end
mitte = (k+1)/2;
A(mitte,mitte-2:mitte+2)=[0 0 1 0 0]; % Korrektur der Matrix A: Lager in der Mitte
b=zeros(k,1);
q=zeros(k,1);
q(mitte:k-2) = 0:q1/(LL/2/deltax):q1;
for i=mitte:k-2
b(i,1)=q(i)*deltax^4/EI; % Beschreibung des Vektors b an der Stelle der
% Streckenlast qi ( q1*l^4/(E*I) wurden im Buch ausgeklammert)
end
b(nA/4+3)=F/deltax*deltax^4/EI; % Verteilung der Kraft F auf einen Abschnitt
% ( q1*l^4/(E*I) wurde ausgeklammert)
% Lösen des Gleichungssystems
v=inv(A)*b; % Berechnung der Durchsenkung
clf;
x = 0:deltax:LL;
plot (x,-v(3:k-2)) % Ausdrucken der Biegelinie
%grid on
ylabel('Verschiebung (mm)')
xlabel('Normierte Balkenlänge')
ErgebnisKnoten28 = v(28)
ErgebnisKnoten78 = v(78)
|
|
|
|
|
Nach dem Starten von MATLAB wird File | Open gewählt und im Fenster “Open” (unter “Dateityp” sollte “All MATLAB Files” eingestellt sein) wird in das Verzeichnis gewechselt, in dem sich die Datei S265.m befindet. Doppelklick auf S265.m öffnet die Datei in einem neuen Fenster.
 In diesem Fenster wird Debug | Run gewählt. Möglicherweise öffnet sich ein Fenster “MATLAB Editor”, in dem man das Angebot “Change MATLAB current directory” annehmen sollte. Danach wird
die Rechnung ausgeführt. In diesem Fenster wird Debug | Run gewählt. Möglicherweise öffnet sich ein Fenster “MATLAB Editor”, in dem man das Angebot “Change MATLAB current directory” annehmen sollte. Danach wird
die Rechnung ausgeführt.
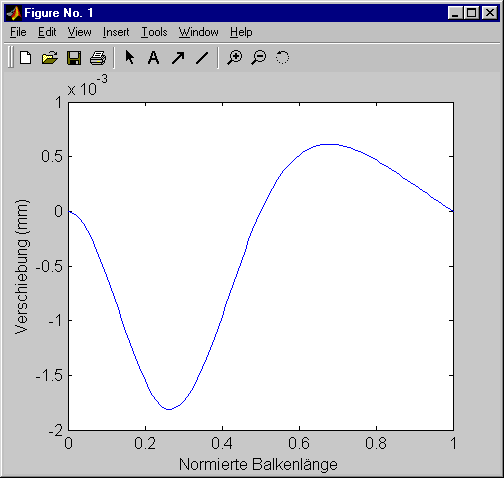
Die mit plot ... eingeleitete Zeile am Ende führt zur graphischen Ausgabe der Biegelinie (nebenstehende Abbildung).
|
|
|
|
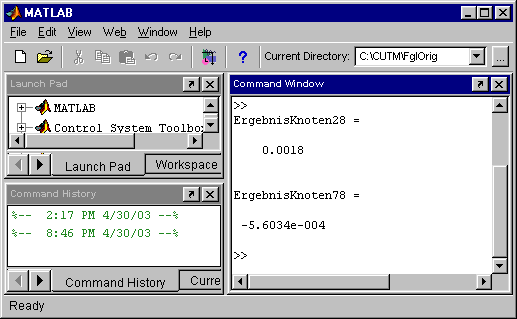 Die beiden letzten Zeilen führen dazu,
dass im “Command window” von MATLAB zwei Ergebnisse angezeigt werden: Durchbiegung unter der Einzelkraft und Durchbiegung in der Mitte der rechten Trägerhälfte (nebenstehende Abbildung). Die beiden letzten Zeilen führen dazu,
dass im “Command window” von MATLAB zwei Ergebnisse angezeigt werden: Durchbiegung unter der Einzelkraft und Durchbiegung in der Mitte der rechten Trägerhälfte (nebenstehende Abbildung).
|
|
|
|
Nachdem man im Fenster, in dem die Datei S265.m angezeigt wird, die entsprechende Zeile auf
lambda = 0;
geändert hat, kann die zweite Rechnung mit Debug | Save and Run gestartet werden.
|
|
|
|
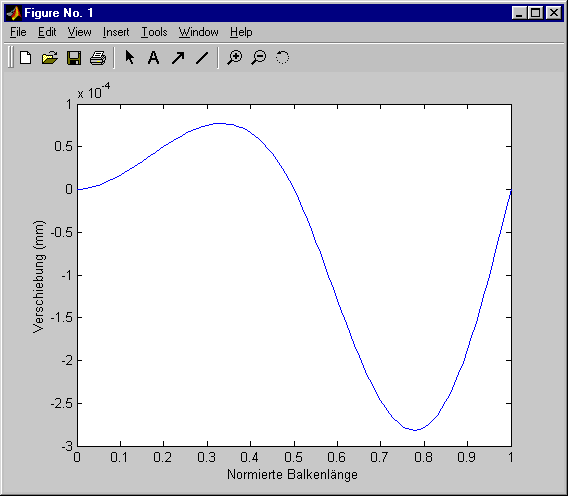 Nebenstehende Abbildung zeigt
das Graphik-Fenster für die Variante λ = 0. Nebenstehende Abbildung zeigt
das Graphik-Fenster für die Variante λ = 0.
|
|
|
|
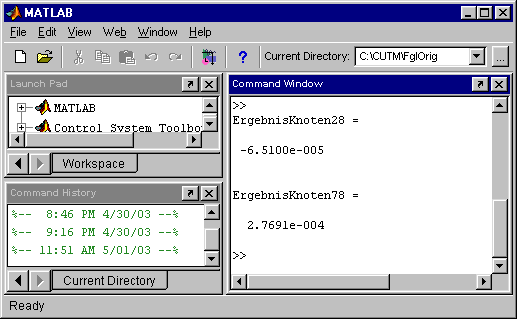 Im “Command window” des MATLAB
-Fensters werden die beiden Durchbiegungen (unter der Einzelkraft und in der Mitte der rechten Trägerhälfte) für den Fall λ = 0 angezeigt. Im “Command window” des MATLAB
-Fensters werden die beiden Durchbiegungen (unter der Einzelkraft und in der Mitte der rechten Trägerhälfte) für den Fall λ = 0 angezeigt.
Diese beiden Werte können mit der exakten Berechnung dieses Falls (Seiten 249 bis 252) verglichen werden. Mit Abweichungen von deutlich weniger als 0,1% von den exakten Werten sind die mit dem
Differenzenverfahren bei der gewählten Einteilung in 100 Abschnitte berechneten Näherungswerte praktisch exakt, so dass auf eine feinere Diskretisierung verzichtet werden kann.
|
|
|
|
|
λ = 0
|
Differenzen-Verfahren (100 Abschnitte)
|
Exakt
|
|
v28
|
- 0,0000651
|
- 0,000065104
|
|
v78
|
0,00027691
|
- 0,000276693
|
|
|
|
|
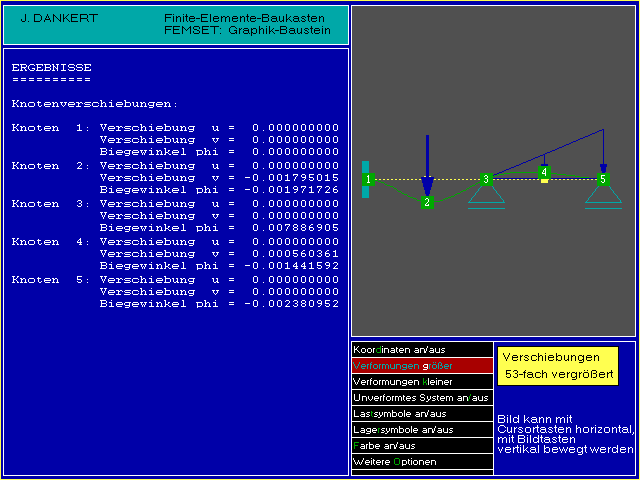
Die gleiche Aussage trifft auch für den Fall mit zusätzlicher Einzelkraft zu (λ
= 2), der als erste Variante berechnet wurde. Hierfür ist allerdings die exakte Berechnung als “Handrechnung” unzumutbar, aber da die Finite-Elemente-Methode für Probleme dieser Art exakte Ergebnisse liefert, wird mit der unten zu sehenden Rechnung (
CAMMPUS-Programm RAHMEN2D) verglichen (die FEM-Werte werden mit geändertem Vorzeichen angegeben, weil das
Programm nach oben gerichtete Verschiebungen als positiv ausgibt):
|
|
|
|
|
λ = 2
|
Differenzen-Verfahren (100 Abschnitte)
|
Exakt (FEM)
|
|
v28 (bzw. v am Knoten 2)
|
0,0018
|
0,001795
|
|
v78 (bzw. v am Knoten 4)
|
- 0,00056034
|
- 0,00056036
|
|
|
|
|
 |
|
|
|
Homepage
|
|
|
|
www.D@nkert.de
|
|
|
 |
|
|
|
|
|
|
 |
|
|
|
|
|
|
|
D
|
 |
|
nkert.de
|
|
|
|
|
|
|
 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|




 In diesem Fenster wird Debug | Run gewählt. Möglicherweise öffnet sich ein Fenster “MATLAB Editor”, in dem man das Angebot “Change MATLAB current directory” annehmen sollte. Danach wird
die Rechnung ausgeführt.
In diesem Fenster wird Debug | Run gewählt. Möglicherweise öffnet sich ein Fenster “MATLAB Editor”, in dem man das Angebot “Change MATLAB current directory” annehmen sollte. Danach wird
die Rechnung ausgeführt.
 Die beiden letzten Zeilen führen dazu,
dass im “Command window” von MATLAB zwei Ergebnisse angezeigt werden: Durchbiegung unter der Einzelkraft und Durchbiegung in der Mitte der rechten Trägerhälfte (nebenstehende Abbildung).
Die beiden letzten Zeilen führen dazu,
dass im “Command window” von MATLAB zwei Ergebnisse angezeigt werden: Durchbiegung unter der Einzelkraft und Durchbiegung in der Mitte der rechten Trägerhälfte (nebenstehende Abbildung). Nebenstehende Abbildung zeigt
das Graphik-Fenster für die Variante λ = 0.
Nebenstehende Abbildung zeigt
das Graphik-Fenster für die Variante λ = 0.  Im “Command window” des MATLAB
-Fensters werden die beiden Durchbiegungen (unter der Einzelkraft und in der Mitte der rechten Trägerhälfte) für den Fall λ = 0 angezeigt.
Im “Command window” des MATLAB
-Fensters werden die beiden Durchbiegungen (unter der Einzelkraft und in der Mitte der rechten Trägerhälfte) für den Fall λ = 0 angezeigt.