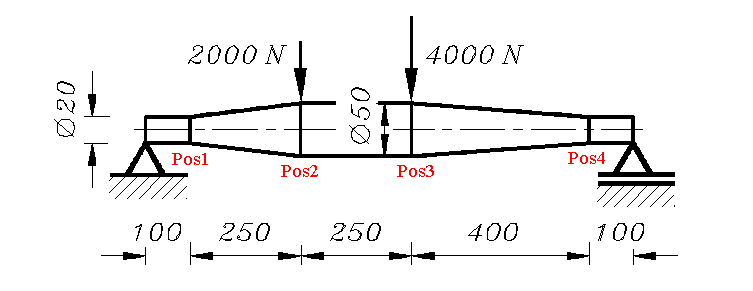
Die auf Seite 712 angegebenen Ergebnisse für die Berechnung der Durchbiegung der stückweise konischen Welle (Elastizitätsmodul: E = 210000 N/mm²) nach der Finite-Elemente-Methode sollen mit dem Differenzenverfahren verifiziert werden.

Die nachfolgend gelistete M-Datei ist so allgemein gehalten, dass die Feinheit der Diskretisierung durch Änderung eines Wertes (nA in der farblich hervorgehobenen Zeile) eingestellt werden kann.

% Aufgabe auf Seite 711 mit Differenzenverfahren mit beliebiger Anzahl von
% Abschnitten nA (sinnvoll ist, nA als Vielfaches von 22 zu wählen, um alle
% markanten Punkte zu treffen)

% Die Hinweise auf Seite 268 ("Bezugs-Biegesteifigkeit") werden beachtet, so dass
% es zu keiner Warnung bei der Lösung des Gleichungssystems kommt

clear all

E  = 210000 ;
F1 = 2000 ;
F2 = 4000 ;

d1 =  20 ;
d2 =  50 ;
EI0 = E*pi*d2^4/64 ;
tl1 = 100 ;
tl2 = 250 ;
tl3 = 250 ;
tl4 = 400 ;
tl5 = 100 ;
tl = tl1 + tl2 + tl3 + tl4 + tl5 ;

nA = 220 ;             % Nur dieser Wert muss geändert werden für feinere Diskretisierung!
n  = nA + 5 ;
z  = 0:tl/nA:tl ;

for i=1:nA+1           % Durchmesser werden nur für die nA+1 Trägerpunkte bestimmt
   if     (z(i) < tl1) d(i) = d1 ;
   elseif (z(i) < tl1+tl2) d(i) = d1 + (d2-d1)/tl2 * (z(i)-tl1) ;
   elseif (z(i) < tl1+tl2+tl3) d(i) = d2 ;
   elseif (z(i) < tl1+tl2+tl3+tl4) d(i) = d2 - (d2-d1)/tl4 * (z(i)-tl1-tl2-tl3) ;
   else   d(i) = d1 ;
   end
end

mu(3:nA+3) = (d/d2).^4 ;               % mu-Werte (Seite 268) werden auch für die ...
mu(2)      = mu(3) ;                   % ... (erforderlichen) Außenpunkte bestimmt
mu(nA+4)   = mu(nA+3) ;

A = zeros (n , n) ;
b = zeros (n , 1) ;

A(1:2,1:5)     = [0 0 1 0 0 ; 0 1 -2 1 0] ;          % Randbedingungen links
A(n-1:n,n-4:n) = [0 0 1 0 0 ; 0 1 -2 1 0] ;          % Randbedingungen rechts

for i=3:n-2                           
  A(i,i-2:i+2)=[mu(i-1) -2*(mu(i-1)+mu(i)) mu(i-1)+4*mu(i)+mu(i+1) -2*(mu(i)+mu(i+1)) mu(i+1)] ;
end

pos2   = nA * (tl1+tl2)/tl + 3 ;
pos3   = nA * (tl1+tl2+tl3)/tl + 3 ;
b(pos2) = F1 * (tl/nA)^3 / EI0 ;
b(pos3) = F2 * (tl/nA)^3 / EI0 ;

v = A \ b ;                      % Lösen des Gleichungssystems

% Biegelinie graphisch darstellen:
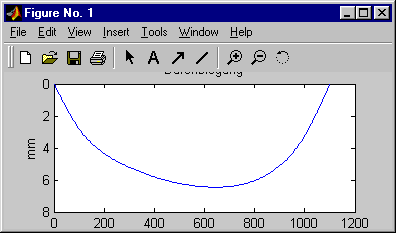
plot(z , v(3:n-2)) , axis ij , title('Durchbiegung') , ylabel('mm') ;

pos1 = nA * (tl1)/tl + 3 ;
pos4 = nA * (tl1+tl2+tl3+tl4)/tl + 3 ;
vAnf = v(3)
vPos1 = v(pos1)
vPos2 = v(pos2)
vPos3 = v(pos3)
vPos4 = v(pos4)
vEnd = v(nA+3)

Die am Ende der Datei farblich hervorgehobenen Zeilen sorgen für die graphische Ausgabe der Biegelinie (Bild unten) und die Ausgabe der Durchbiegung an den markanten Punkten (in das “Command Window”, Bild rechts), die auch auf Seite 712 angegeben sind (jeweils die Stellen des Übergangs vom konstanten Querschnitt auf einen veränderlichen Querschnitt bzw. umgekehrt). Diese Ergebnisse wurden mit einer Einteilung des Trägers in insgesamt 220 Abschnitte (entsprechend dem Wert für nA in der oben zu sehenden Datei) ermittelt.

Die folgende Tabelle gibt die Ergebnisse für unterschiedlich feine Diskretisierung im Vergleich mit der FEM Rechnung mit 35 speziellen Elementen an.

Homepage

www.D@nkert.de

D

nkert.de