Das Beispiel

Die Aufgabe, die dem hier beschriebenen Problem zugrunde liegt, ist eigentlich nicht von Interesse. Es soll mit ihr nur gezeigt werden, dass es durchaus kein spitzfindig konstruiertes Problem ist, mit dem die Matrix erzeugt wird, die eine falsche Determinante liefert.

Für den im Bild zu sehenden Biegeträger gelten die folgenden sinnvollen Parameter:

l = 1000 mm   ;   EI = 2 · 10¹⁰ Nmm²   ;   q₀ = 2 N/mm .

Der Träger ist - wie unschwer zu erkennen ist - nicht ausreichend gelagert, um tragfähig sein. Eine Finite-Elemente-Berechnung eines solchen Systems führt deshalb auf ein Gleichungssystem mit einer singulären Koeffizientenmatrix. Im folgenden Matlab-Script wird das FEM-Gleichungssystem aufgebaut, die Koeffizientenmatrix wird auf Singularität (Berechnung des Wertes ihrer Determinante) getestet.

Berechnung der Determinante

Der Aufbau des Gleichungssystems in den Zeilen 4 bis 6 des nebenstehend zu sehenden Scripts ist für die Betrachtungen hier uninteressant (für Interessenten: Matlab-Femset).

Die Koeffizientenmatrix wird in Zeile 6 in das Command Window ausgegeben. In Zeile 8 wird ihre Determinante berechnet und ausgegeben.

In Zeile 9 wird der Rang der Matrix mit der Matlab-Function rank berechnet und ausgegeben.

Die in Zeile 10 aufgerufene Matlab-Function rref erzeugt mit dem Gauß-Jordan-Algorithmus die "reduced row echelon form" der Matrix, die auch den Rang der Matrix erkennen lässt.

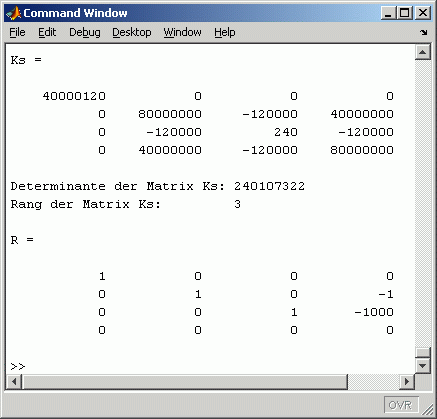Im Command Window findet man die Ergebnisse der Berechnung:

• Der berechnete Wert der Determinante wird mit 240 107 322 ausgewiesen. Dass er deutlich größer ist als das größte Matrixelement, ist nicht verdächtig (und eigentlich eher der Regelfall). Dass er aber falsch ist, könnte selbst ein wenig geübter Rechner in weniger als 5 Minuten per Handrechnung nachweisen.
   
• Der Rang der vierreihigen Matrix wird mit 3 ausgewiesen, das heißt: Singularität und damit "Determinante gleich Null".
   
• Das nachfolgend mit rref berechnete "Gauß-Jordan-Ergebnis" zeigt die Singularität der Matrix dadurch, dass eine komplette Nullzeile entstanden ist.
   

Fazit: Die beiden Functions rank und rref erkennen die Singularität der Matrix, det liefert für den Wert der Determinante ein völlig falsches Ergebnis ab.