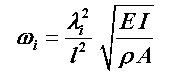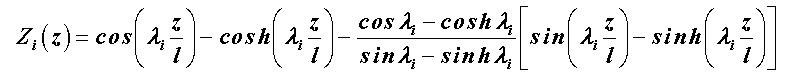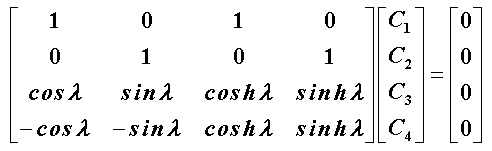|
 |
||||||
|
Im Skript “Biegeschwingungen gerader Träger” wird diese Aufgabe als Beispiel ausführlich behandelt. Es wird gezeigt, dass sich die Eigenkreisfrequenzen nach der Formel
mit den λi-Werten berechnen lassen, die sich als Lösungen der Eigenwertgleichung
ergeben. Die bis auf einen beliebigen Faktor bestimmbaren Eigenschwingungsformen lassen sich dann nach
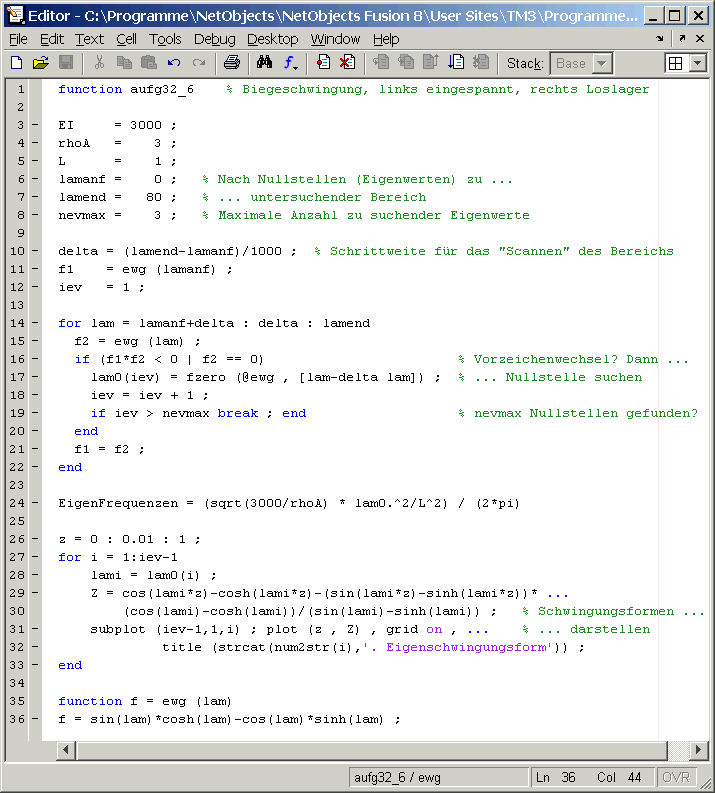
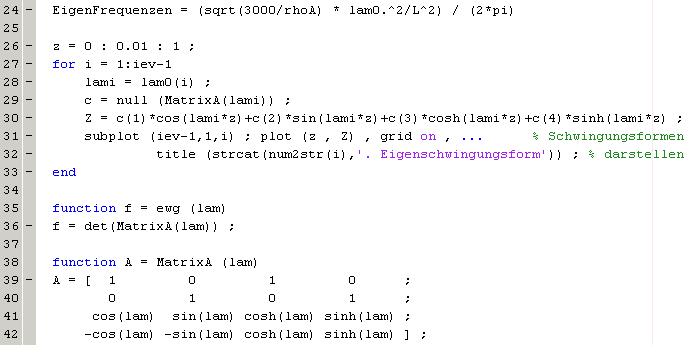
berechnen. Das nachfolgende MATLAB-Script realisiert diese Berechnung:
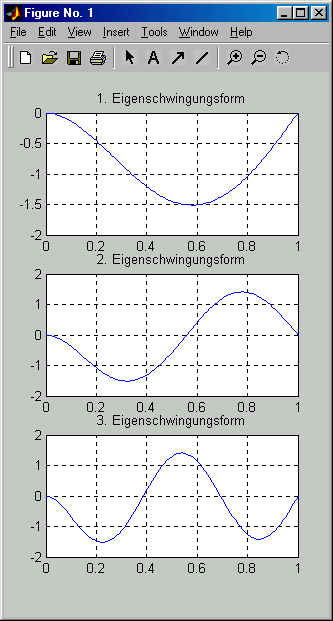
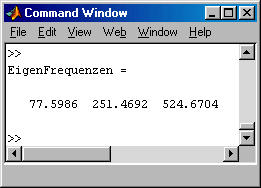
Die Ergebnisse findet man in einem Graphik-Fenster und im Command Window:
Diese Berechnung erfordert eine umfangreiche Handrechnung. In dem Skript “Biegeschwingungen gerader Träger ” wird auch gezeigt, dass man durchaus bereits die Nullstellenberechnung bei der Determinante der Koeffizientenmatrix des homogenen Gleichungssystems
starten kann (die oben angegebene Eigenwertgleichung ergab sich aus der Entwicklung dieser Determinante). Dann kann man auch die Schwingungsformen auf einfachere Art ermitteln (hierfür wird auf die Darstellung in dem genannten Skript verwiesen). Im oben gelisteten MATLAB-Script ergeben sich Änderungen ab Zeile 29. Diese Variante kommt mit wesentlich weniger (aufwändiger und damit fehleranfälliger) Handrechnung aus:
|
|||||||
|
|||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||