|
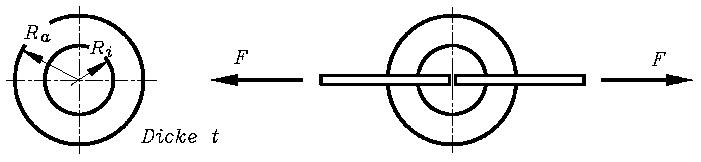
Ein Kettenglied in Form einer gelochten Kreisscheibe wird durch die Zugkräfte F belastet. Man ermittle nach der Theorie des stark gekrümmten Trägers
- den Verlauf der Radialverschiebung,
- die Verläufe von Biegemoment und Normalkraft und die maximalen Normalspannungen in den beiden Symmetrieschnitten des Kettenglieds,
- die horizontale Vergrößerung und die vertikale Verjüngung des Durchmessers.
Gegeben: F = 1000 N ; Ra = 62 mm ; Ri = 42 mm ; t = 5 mm ;
ν = 0,3 ; E = 210000 N/mm2 .
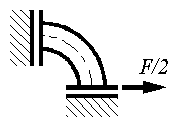  Wegen der doppelten Symmetrie braucht nur ein Viertel eines Kettengliedes
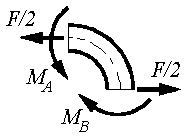
betrachtet zu werden (Skizze links). In der Skizze rechts sieht man das Symmetrieviertel mit den “Lagerreaktionen” in den Symmetrieschnitten, wobei die
beiden Kraft-Gleichgewichtsbedingungen bereits ausgenutzt wurden. Es verbleiben zwei unbekannte “Einspannmomente”, für die nur noch eine Gleichgewichtsbedingung zur Verfügung steht: Das Problem ist einfach statisch
unbestimmt. Wegen der doppelten Symmetrie braucht nur ein Viertel eines Kettengliedes
betrachtet zu werden (Skizze links). In der Skizze rechts sieht man das Symmetrieviertel mit den “Lagerreaktionen” in den Symmetrieschnitten, wobei die
beiden Kraft-Gleichgewichtsbedingungen bereits ausgenutzt wurden. Es verbleiben zwei unbekannte “Einspannmomente”, für die nur noch eine Gleichgewichtsbedingung zur Verfügung steht: Das Problem ist einfach statisch
unbestimmt.
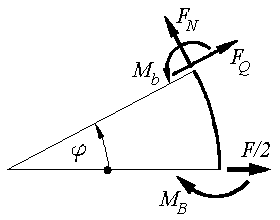 Nebenstehend sind vergrößert die Schnittgrößen in Abhängigkeit von einer Winkelkoordinate zu
sehen. Normalkraft und Biegemoment ergeben sich aus Gleichgewichtsbedingungen zu: Nebenstehend sind vergrößert die Schnittgrößen in Abhängigkeit von einer Winkelkoordinate zu
sehen. Normalkraft und Biegemoment ergeben sich aus Gleichgewichtsbedingungen zu:
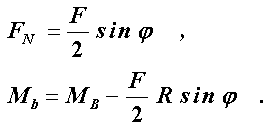
Diese Beziehugen können in die Differenzialgleichungen für die Verformungsberechnug des
Kreisbogenträgers (z. B. Formel 19.18 in “Dankert/Dankert. Technische Mechanik”) eingesetzt werden:
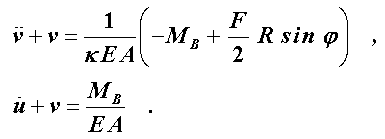
In diesen Differenzialgleichungen ist u die Tangentialverschiebung, v die Radialverschiebung, E der Elastizitätsmodul, A
die Querschnittsfläche (hier: A = (Ra-Ri) t = 100 mm2), R der Radius der Schwerpunktfaser (hier: R = (Ri+Ra)/2 = 52 mm
) und κ der Querschnittsparameter für den gekrümmten Träger, der sich für den Rechteckquerschnitt nach der Formel (siehe z. B. “Dankert/Dankert. Technische Mechanik”, Seite 309)
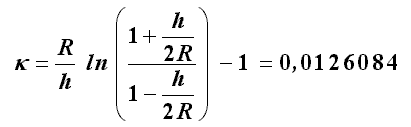
berechnen lässt (mit der Höhe des Rechteckquerschnitts, der für das aktuelle Problem h = Ra-Ri = 20 mm beträgt).
Die erste der beiden Differenzialgleichungen ist eine inhomogene lineare Differenzialgleichung zweiter Ordnung mit konstanten Koeffizienten. In
“Dankert/Dankert. Technische Mechanik” werden auf Seite 318 allgemeine Hinweise zum Finden einer Partikulärlösung und damit auch zur
allgemeinen Lösung dieser Differenzialgleichung gegeben. Sie lautet für das hier behandelte Problem:
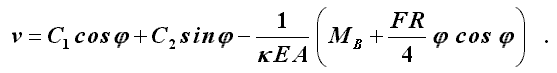
Diese Lösung kann in die oben angegebene zweite Differenzialgleichung eingesetzt werden, und man erhält durch eine einfache Integration, bei der
eine weitere Integrationskonstante erzeugt wird, die allgemeine Lösung für die Tangentialverschiebung:
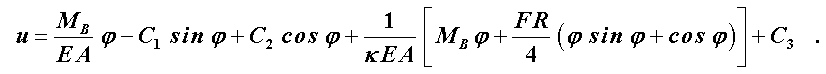
Diese beiden allgemeinen Lösungen enthalten neben den drei Integrationskonstanten das unbekannte Moment MB, so dass vier Randbedingungen
erforderlich sind (hier: Tangentialverschiebung in beiden Symmetrieschnitten gleich Null und erste Ableitung der Radialverschiebung in beiden Symmetrieschnitten ebenfalls Null):
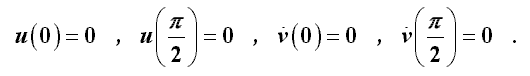
Nach einfacher, aber etwas mühsamer Rechnung erhält man:
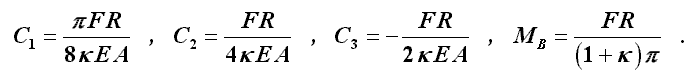
Damit ergeben sich die Funktionen für die Radialverschiebung
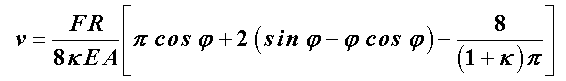
und das Biegemoment
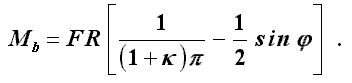
Die Spannungen in einem Querschnitt können nach der Formel (vgl. z. B. “Dankert/Dankert. Technische Mechanik”, Seite 309)
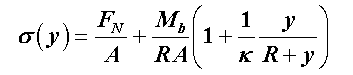
berechnet werden. Hierin ist y die Querschnittskoordinate, die ihren Ursprung im Schwerpunkt des Querschnitts hat und nach außen gerichtet ist
(für das aktuelle Problem liegt also der Punkt am Innenradius bei y = -10 mm, der Punkt am Außenradius bei y = 10 mm).
Das maximale Biegemoment tritt bei φ = 0 (Punkt B) auf, dort verschwindet die Normalkraft:
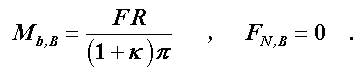
In diesem Querschnitt ergibt sich am Innenrand die Spannung σB,i = - 56,2 N/mm2, am Außenrand errechnet man
σB,a = 43,4 N/mm2.
Die maximale Normalkraft findet man bei φ = π/2 (Punkt A):
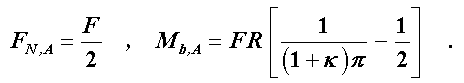
In diesem Querschnitt ergibt sich am Innenrand die Spannung σA,i = 38,2 N/mm2, am Außenrand errechnet man
σA,a = - 20,6 N/mm2.
Die Vergrößerung des Durchmessers in horizontaler Richtung erhält man mit der oben bereits angegebenen Formel für die Radialverschiebung zu
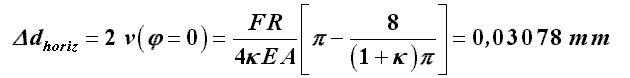
und die Verjüngung des Durchmessers in vertikaler Richtung kann mit der gleichen Formel zu
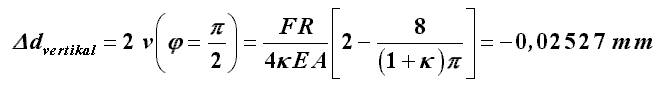
berechnet werden.
Die gleiche Aufgabe ist mit dem Matlab-Femset-Interface mit der Finite-Elemente-Methode berechnet worden. Ein Vergleich der Ergebnisse zeigt, dass die Theorie des gekrümmten Trägers sowohl für die Verformungs- als auch für die Spannungsberechnung sehr gute Ergebnisse liefert.
|

