|
% Aufgabe 19-3 mit dem Differenzenverfahren (die Symmetrie des Problems
% wird nicht genutzt, um komplette graphische Darstellungen zu erzielen).
% Das Script ist bewusst allgemein gehalten, so dass es auch als Vorlage
% dienen kann, wenn Linienlast, Biegesteifigkeit und Bettungszahl
% veraenderlich sind:
clear all
L = 1 ;
a = L/4 ;
EI = 1 ;
F = 1 ;
k = 2 ;
Lges = 2*L ;
EIB = EI ; % Bezugs-Biegesteifigkeit
nA = 2000 ; % Anzahl der Abschnitte
n = nA + 5 ; % Anzahl der Gleichungen
h = Lges / nA ; % Schrittweite
A = zeros (n,7) ; % Rechteckmatrix fuer Aufnahme der Bandmatrix
b = zeros (n,1) ; % Nullvektor ("rechte Seite")
qi = zeros (n,1) ; % Linienlastintensitaeten an Stuetzpunkten
mi = zeros (n,1) ; % EIi = mi * EIB
ki = zeros (n,1) ; % Bettungszahlen an Stuetzpunkten
% Markante Punkte:
iF1 = round (nA*a/Lges+3.1) ;
iF2 = round (nA*(Lges-a)/Lges+3.1) ;
iMitte = round (nA*0.5+3.1) ;
iRechts = n - 2 ;
% Belastung
qi(iF1) = F/h ;
qi(iF2) = F/h ;
% Biegesteifigkeit (mue-Werte):
mi(1:n) = 1 ;
% Bettungszahl (ki-Werte):
ki(1:n) = k ;
%Randbedingungen:
A(1:2,:) = [0 0 0 0 mi(3) -2*mi(3) mi(3) ;
0 0 mi(2) -2*mi(2) mi(2)-mi(4) 2*mi(4) -mi(4)] ; % Freier Rand links und freier Rand rechts
A(n-1:n,:) = [mi(iRechts-1) -2*mi(iRechts-1) mi(iRechts-1)-mi(iRechts+1) 2*mi(iRechts+1) -mi(iRechts+1) 0 0 ;
mi(iRechts) -2*mi(iRechts) mi(iRechts) 0 0 0 0] ;
for i = 3:n-2 % Matrix A:
A(i,:)= [0 mi(i-1) -2*(mi(i-1)+mi(i)) mi(i-1)+4*mi(i)+mi(i+1)+ki(i)*h^4/EIB -2*(mi(i)+mi(i+1)) mi(i+1) 0] ;
b(i) = qi(i)*h^4/(EIB) ; % Standardgleichungen
end
t1 = cputime ;
v = gabamp (A , b) ; % Berechnung der Durchsenkung
ZeitGlSyst = cputime - t1
clf;
z = 0 : h : Lges ;
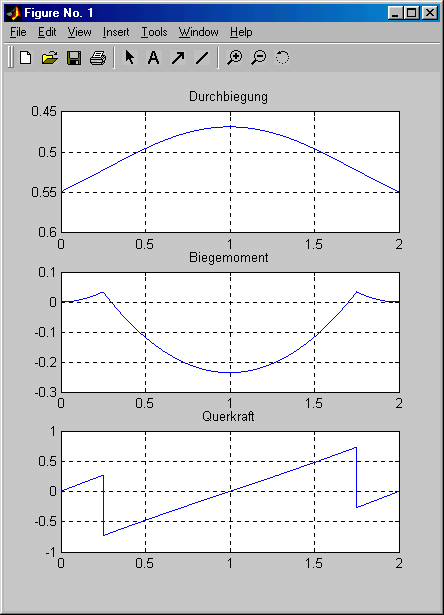
subplot (3,1,1) ; plot (z , v(3:n-2)) , axis ij , grid on ,
title ('Durchbiegung') % Graphische Ausgabe der Biegelinie
for i=3:n-2
Mb(i) = -mi(i)*EIB * (v(i-1)-2*v(i)+v(i+1))/h^2 ; % Biegemoment
FQ(i) = 0.5*EIB * (mi(i-1)*v(i-2)-2*mi(i-1)*v(i-1)+(mi(i-1)-mi(i+1)) ...
*v(i)+2*mi(i+1)*v(i+1)-mi(i+1)*v(i+2))/h^3 ; % Querkraft
end
subplot (3,1,2) ; plot (z , Mb(3:n-2)) , grid on , title ('Biegemoment')
subplot (3,1,3) ; plot (z , FQ(3:n-2)) , grid on , title ('Querkraft')
vRand = v(3) % Ausgabe in das Command window:
vMitte = v(iMitte) % Spezielle Wert fuer v und Mb
MbF = Mb(iF1)
MbMitte = Mb(iMitte)
|